
【题目】如图,四边形![]() 内接于半圆
内接于半圆![]() ,
,![]() 为直径,
为直径,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点F.若
于点F.若![]() ,
,![]() ,则
,则![]() 的长为 ( )
的长为 ( )
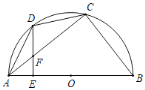
A.8B.10C.15D.24
【答案】D
【解析】
连接BD,如图,先利用圆周角定理证明∠ADE=∠DAC得到FD=FA=5,再根据余弦的定义计算出AE=3,则EF=4,DE=9,接着证明ΔADEΔDBE,利用相似比得到BE=27,所以AB=30,然后在RtΔABC中利用余弦定义计算出BC=24的长.
连接BD,如图,
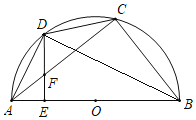
∵AB为直径,
∴∠ADB=∠ACB=90°,
∵AD=CD,
∴∠DAC=∠DCA,
而∠DCA=∠ABD,
∴∠DAC=∠ABD,
∵DE⊥AB,
∴∠ABD+∠BDE=90°,
而∠ADE+∠BDE=90°,
∴∠ABD=∠ADE,
∴∠ADE=∠DAC,
∴FD=FA=5,
在RtΔAEF中,∵cos∠CAB=![]() =
=![]() ,
,
∴AE=3,
∴EF=![]() =4,DE=5+4=9,
=4,DE=5+4=9,
∵∠ADE=∠DBE,∠AED=∠BED,
∴ΔADEΔDBE,
∴DE:BE=AE:DE,即9:BE=3:9,
∴BE=27,
∴AB=3+27=30,
在RtΔABC中,∵cos∠CAB=![]() =
=![]() ,
,
∴AC=30×![]() =18,
=18,
BC=![]() =
=![]() =24,
=24,
故选D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
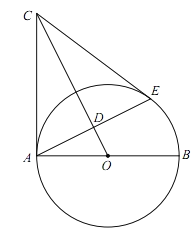
【题目】已知:如图,AB是⊙O的直径,点C是过点A的⊙O的切线上一点,连接OC,过点A作OC的垂线交OC于点D,交⊙O于点E,连接CE.
(1)求证:CE与⊙O相切;
(2)连结BD并延长交AC于点F,若OA=5,sin∠BAE=![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
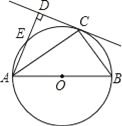
【题目】如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
(1)求证:AC平分∠BAD;
(2)若CD=3,AC=3![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
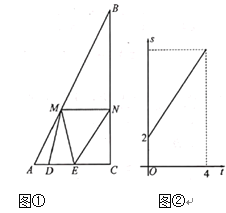
【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向匀速运动,速度为1
方向匀速运动,速度为1![]() 点
点![]() 是
是![]() 上位于点
上位于点![]() 右侧的动点,点
右侧的动点,点![]() 是
是![]() 上的动点,在运动过程中始终保持
上的动点,在运动过程中始终保持![]() ,
,![]() cm.过
cm.过![]() 作
作![]() 交
交![]() 于
于![]() ,当点
,当点![]() 与点
与点![]() 重合时点
重合时点![]() 停止运动.设
停止运动.设![]() 的而积为
的而积为![]() ,点
,点![]() 的运动时问为
的运动时问为![]() ,
,![]() 与
与![]() 的函数关系如图②所示:
的函数关系如图②所示:
(1)![]() =_______
=_______![]() ,
,![]() =_______
=_______![]() ;
;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
(3)是否存在![]() 的值,使得以
的值,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?如果存在,求
相似?如果存在,求![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生到恩格贝![]() 和康镇
和康镇![]() 进行研学活动,澄澄老师在网上查得,
进行研学活动,澄澄老师在网上查得,![]() 和
和![]() 分别位于学校
分别位于学校![]() 的正北和正东方向,
的正北和正东方向,![]() 位于
位于![]() 南偏东37°方向,校车从
南偏东37°方向,校车从![]() 出发,沿正北方向前往
出发,沿正北方向前往![]() 地,行驶到15千米的
地,行驶到15千米的![]() 处时,导航显示,在
处时,导航显示,在![]() 处北偏东45°方向有一服务区
处北偏东45°方向有一服务区![]() ,且
,且![]() 位于
位于![]() ,
,![]() 两地中点处.
两地中点处.
(1)求![]() ,
,![]() 两地之间的距离;
两地之间的距离;
(2)校车从![]() 地匀速行驶1小时40分钟到达
地匀速行驶1小时40分钟到达![]() 地,若这段路程限速100千米/时,计算校车是否超速?
地,若这段路程限速100千米/时,计算校车是否超速?
(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=2x+b与反比例函数y=![]() 的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E,
的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E,
(1)若k=8,且点A的横坐标为1,求b的值;
(2)已知△BEC的面积为4,则k的值为多少?
(3)若将直线旋转,k=8,点E为△ABC的重心且OE=2,求直线AC的解析式.
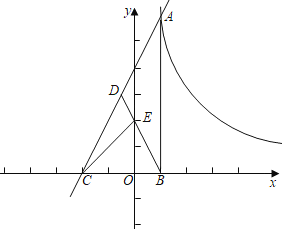
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=mx2﹣2mx﹣3m与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,连接AC,BC,将△OBC沿BC所在的直线翻折,得到△DBC,连接OD.
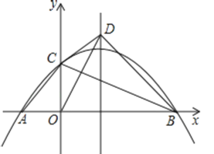
(1)点A的坐标为 ,点B的坐标为 .
(2)如图,若点D落在抛物线的对称轴上,且在x轴上方,求抛物线的解析式.
(3)设△OBD的面积为S1,△OAC的面积为S2,若S1=![]() S2,求m的值.
S2,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是
是![]() 的内接四边形,四边形
的内接四边形,四边形![]() 两组对边的延长线分别相交于点
两组对边的延长线分别相交于点![]() ,
,![]() ,且
,且![]() ,
,![]() ,连接
,连接![]() .
.

(1)求![]() 的度数;
的度数;
(2)当![]() 的半径等于2时,请直接写出
的半径等于2时,请直接写出![]() 的长.(结果保留
的长.(结果保留![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com