
【题目】已知直线y=2x+b与反比例函数y=![]() 的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E,
的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E,
(1)若k=8,且点A的横坐标为1,求b的值;
(2)已知△BEC的面积为4,则k的值为多少?
(3)若将直线旋转,k=8,点E为△ABC的重心且OE=2,求直线AC的解析式.
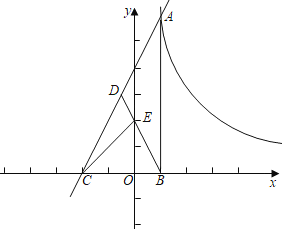
【答案】(1)b=6;(2)k=8;(3)直线AC的解析式为y=2x+4.
【解析】
(1)求出点A的坐标,利用待定系数法即可解决问题.
(2)设A(m,![]() ),则B(m,0),构建一次函数求出点E,点C的坐标(用m,k表示),再利用三角形的面积,构建方程求出k即可.
),则B(m,0),构建一次函数求出点E,点C的坐标(用m,k表示),再利用三角形的面积,构建方程求出k即可.
(3)连接AE,延长AE交BC于J.求出点J的坐标,再根据中点坐标公式构建方程求出k即可解决问题.
解:(1)由题意,A(1,8),
把A(1,8)代入y=2x+b得到b=6.
(2)设A(m,![]() ),则B(m,0),
),则B(m,0),
把A(m,![]() )代入y=2x+b得到b=
)代入y=2x+b得到b=![]() ﹣2m,
﹣2m,
∴直线AC的解析式为y=2x+![]() ﹣2m,
﹣2m,
令y=0,得到x=m﹣![]() ,
,
∴C(m﹣![]() ,0),
,0),
∵AD=DC,
∴D(m﹣![]() ,
,![]() ),
),
设直线BD的解析式为y=k′x+b′,
则有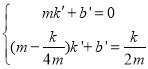 ,
,
解得![]() ,
,
∴直线BD的解析式为y=﹣2x+2m,
∴E(0,2m),
∴OE=2m,BC=OC+OB=![]()
∵S△ECB=4,
∴![]() BCEO=4,
BCEO=4,
∴![]() ×
×![]() ×2m=4,
×2m=4,
∴k=8.
(3)连接AE,延长AE交BC于J.
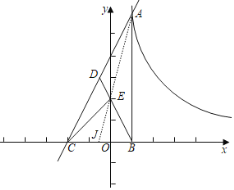
由(2)可知,E(0,2m),
∵OE=2,
∴2m=2,
∴m=1,
∴C((1﹣![]() ,0),B(1,0),A(1,k),
,0),B(1,0),A(1,k),
∴直线AE的解析式为:y=(k﹣2)x+2,
令y=0,得到x=![]() ,
,
∴J(![]() ,0),
,0),
∵E是△ABC的重心,
∴CJ=JB,
∴![]() =
=![]() (1+1﹣
(1+1﹣![]() ),
),
解得k=6或0(舍弃),
∴直线AC的解析式为y=2x+4.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
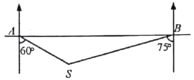
【题目】一艘轮船在![]() 处测得灯塔
处测得灯塔![]() 在船的南偏东60°方向,轮船继续向正东航行30海里后到达
在船的南偏东60°方向,轮船继续向正东航行30海里后到达![]() 处,这时测得灯塔
处,这时测得灯塔![]() 在船的南偏西75°方向,则灯塔
在船的南偏西75°方向,则灯塔![]() 离观测点
离观测点![]() 、
、![]() 的距离分别是( )
的距离分别是( )
A.![]() 海里、15海里B.
海里、15海里B.![]() 海里、15海里
海里、15海里
C.![]() 海里、
海里、![]() 海里D.
海里D.![]() 海里、
海里、![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数![]() 的四个命题:
的四个命题:
①当x=0时,y有最小值12;
②n为任意实数,x=3+n时的函数值大于x=3-n时的函数值;
③若n>3,且n是整数,当![]() 时,y的整数值有
时,y的整数值有![]() 个;
个;
④若函数图象过点![]() 和
和![]() ,其中a>0,b>0,则a<b.
,其中a>0,b>0,则a<b.
其中真命题的序号是( )
A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
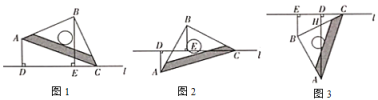
【题目】综合与实践:
如图1,将一个等腰直角三角尺![]() 的顶点
的顶点![]() 放置在直线
放置在直线![]() 上,
上,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
观察发现:
(1)如图1.当![]() ,
,![]() 两点均在直线
两点均在直线![]() 的上方时,
的上方时,
①猜测线段![]() ,
,![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②直接写出线段![]() ,
,![]() 与
与![]() 的数量关系;
的数量关系;
操作证明:
(2)将等腰直角三角尺![]() 绕着点
绕着点![]() 逆时针旋转至图2位置时,线段
逆时针旋转至图2位置时,线段![]() ,
,![]() 与
与![]() 又有怎样的数量关系,请写出你的猜想,并写出证明过程;
又有怎样的数量关系,请写出你的猜想,并写出证明过程;
拓广探索:
(3)将等腰直角三用尺![]() 绕着点
绕着点![]() 继续旋转至图3位置时,
继续旋转至图3位置时,![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江苏省常州市)为了解某校学生的课余兴趣爱好情况,某调查小组设计了“阅读”、“打球”、“书法”和“其他”四个选项,用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况(每个学生必须选一项且只能选一项),并根据调查结果绘制了如下统计图:
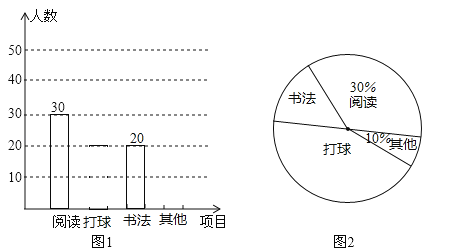
根据统计图所提供的信息,解答下列问题:
(1)本次抽样调查中的样本容量是 ;
(2)补全条形统计图;
(3)该校共有2000名学生,请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
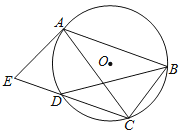
【题目】如图,四边形ABCD内接于⊙O,且AB=AC.延长CD至点E,使CE=BD,连接AE.
(1)求证:AD平分∠BDE;
(2)若AB//CD,求证:AE是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com