
【题目】如图,数轴上点A,B分别对应数a,b.其中a<0,b>0.
(1)当a=﹣2,b=6时,线段AB的中点对应的数是 ;(直接填结果)
(2)若该数轴上另有一点M对应着数m.
①当m=2,b>2,且AM=2BM时,求代数式a+2b+20的值;
②当a=﹣2,且AM=3BM时,小安演算发现代数式3b﹣4m是一个定值.
老师点评:你的演算发现还不完整!
请通过演算解释:为什么“小安的演算发现”是不完整的?
![]()
【答案】(1)2;(2)见解析.
【解析】
(1)首先根据数轴的性质,即可得出中点对应的数值;
(2)①首先判定点M在点A,B之间,然后根据等式列出关系式,即可得解;
②根据题意,分两种情况进行求解:点M在点A,B之间和点M在点B右侧时,通过列出等式,即可判定.
(1)由题意得出,线段AB的中点对应的数是2,
故答案为2;
(2)①当m=2,b>2时,点M在点A,B之间,
∵AM=2BM,
∴m﹣a=2(b﹣m),
∴2﹣a=2(b﹣2),
∴a+2b=6,
∴a+2b+20=6+20=26;
②小安只考虑了一种情况,故老师点评“小安的演算发现”是不完整的.
当点M在点A,B之间时,a=﹣2,
∵AM=3BM,
∴m+2=3(b﹣m),
∴m+2=3b﹣3m,
∴3b﹣4m=2,
∴代数式3b﹣4m是一个定值.
当点M在点B右侧时,
∵AM=3BM,
∴m+2=3(m﹣b),
∴m+2=3m﹣3b,
∴2m﹣3b=2,
∴代数式2m﹣3b也是一个定值.


科目:初中数学 来源: 题型:
【题目】点A、B、C在数轴上表示的数分别为a,b,c,且a,b,c满足(b+2)2+(c﹣24)2=0,多项式x|a+3|y2﹣ax3y+xy2﹣1是五次四项式.
(1)a的值为 ,b的值为 ,c的值为 ;
(2)若数轴上有三个动点M、N、P,分别从点A、B、C开始同时出发在数轴上运动,速度分别为每秒1个单位长度、7个单位长度3个单位长度.
①若点P向左运动,点M向右运动,点N先向左运动,遇到点M后回头再向右运动,遇到点P后又回头再向左运动,……,这样直到点P遇到点M时三点都停止运动,求点N所走的路程;
②若点M、N向右运动,点P向左运动,点Q为线段PN中点,在运动过程中,OQ﹣![]() MN的值是否发生变化?若不变,求其值;若变化,说明理由.
MN的值是否发生变化?若不变,求其值;若变化,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x小时,两车之间的距离为y千米,图中的折线表示y与x之间的函数关系.当两车之间的距离首次为300千米时,经过_____小时后,它们之间的距离再次为300千米.
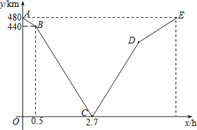
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简求值:
(1)(﹣2)2×5﹣(﹣2)3÷4;
(2)(﹣10)3+[(﹣4)2﹣(1﹣32)×2];
(3)求代数式3a+abc﹣![]() (9a﹣c2)的值,其中a=﹣
(9a﹣c2)的值,其中a=﹣![]() ,b=2,c=﹣3.
,b=2,c=﹣3.
(4)先化简再求值:![]() ,其中x=﹣2,y=
,其中x=﹣2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
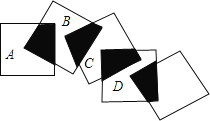
A.2cm2 B.4cm2 C.6cm2 D.8cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班一次数学检测中,共出了20道题,总分为100分,现从中抽出5份试卷进行分析.如图表所示:
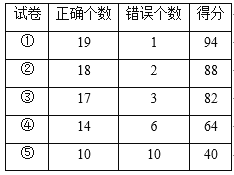
(1)某同学得了70分,他答对了试卷多少道题?
(2)有一同学H他得了76分,另一同学G说他得了72分,谁说的对了?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一次函数![]() 的图象上,它们的横坐标依次为
的图象上,它们的横坐标依次为![]() ,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )

A. 1 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
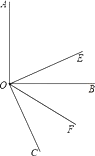
【题目】如图,已知∠AOB是直角,OE平分∠AOC,OF平分∠BOC.
(1)若∠BOC=60°,求∠EOF的度数;
(2)若∠AOC=x°(x>90),此时能否求出∠EOF的大小,若能,请求出它的数值
查看答案和解析>>
科目:初中数学 来源: 题型:
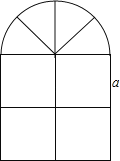
【题目】窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是acm,计算:
(1)窗户的面积;
(2)窗户的外框的总长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com