
ЁОЬтФПЁПЕуAЁЂBЁЂCдкЪ§жсЩЯБэЪОЕФЪ§ЗжБ№ЮЊaЃЌbЃЌcЃЌЧвaЃЌbЃЌcТњзуЃЈb+2ЃЉ2+ЃЈcЉ24ЃЉ2ЃН0ЃЌЖрЯюЪНx|a+3|y2Љax3y+xy2Љ1ЪЧЮхДЮЫФЯюЪНЃЎ
ЃЈ1ЃЉaЕФжЕЮЊЁЁ ЁЁЃЌbЕФжЕЮЊЁЁ ЁЁЃЌcЕФжЕЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєЪ§жсЩЯгаШ§ИіЖЏЕуMЁЂNЁЂPЃЌЗжБ№ДгЕуAЁЂBЁЂCПЊЪМЭЌЪБГіЗЂдкЪ§жсЩЯдЫЖЏЃЌЫйЖШЗжБ№ЮЊУПУы1ИіЕЅЮЛГЄЖШЁЂ7ИіЕЅЮЛГЄЖШ3ИіЕЅЮЛГЄЖШЃЎ
ЂйШєЕуPЯђзѓдЫЖЏЃЌЕуMЯђгвдЫЖЏЃЌЕуNЯШЯђзѓдЫЖЏЃЌгіЕНЕуMКѓЛиЭЗдйЯђгвдЫЖЏЃЌгіЕНЕуPКѓгжЛиЭЗдйЯђзѓдЫЖЏЃЌЁЁЃЌетбљжБЕНЕуPгіЕНЕуMЪБШ§ЕуЖМЭЃжЙдЫЖЏЃЌЧѓЕуNЫљзпЕФТЗГЬЃЛ
ЂкШєЕуMЁЂNЯђгвдЫЖЏЃЌЕуPЯђзѓдЫЖЏЃЌЕуQЮЊЯпЖЮPNжаЕуЃЌдкдЫЖЏЙ§ГЬжаЃЌOQЉ![]() MNЕФжЕЪЧЗёЗЂЩњБфЛЏЃПШєВЛБфЃЌЧѓЦфжЕЃЛШєБфЛЏЃЌЫЕУїРэгЩЃЎ
MNЕФжЕЪЧЗёЗЂЩњБфЛЏЃПШєВЛБфЃЌЧѓЦфжЕЃЛШєБфЛЏЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЉ6ЃЌЉ2ЃЌ24ЃЛЃЈ2ЃЉЂй52.5ЕЅЮЛГЄЖШЃЛЂкВЛЗЂЩњБфЛЏЃЌРэгЩЯъМћНтЮіЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЗЧИКЪ§ЕФаджЪЧѓГіbгыcЕФжЕЃЌИљОнЖрЯюЪНЮЊЮхДЮЫФЯюЪНЧѓГіaЕФжЕЃЛ
ЃЈ2ЃЉЂйгЩЬтвтЧѓГіЕуPгіЕНЕуMЕФЪБМфЃЌвВОЭЪЧЕуNЕФдЫЖЏЪБМфЃЌЪзЯШЧѓГіACЕФОрРыЃЌЩшЯргіЪБМфЮЊtЃЌЗжБ№БэЪОГіСНЕуааЪЛЕФОрРыЃЌНЈСЂЗНГЬНтОіЮЪЬтМДПЩЃЛ
ЂкЩшдЫЖЏЕФЪБМфЮЊtУыЃЌдђMNЃНЃЈ7Љ1ЃЉt+4ЃН6t+4ЃЌгУКЌtЕФЪНзгЗжБ№БэЪОГіЕуNКЭЕуPЃЌНјЖјБэЪОГіЕуQЃЌгЩгкЕуNдЫЖЏЕФПьЃЌЧвЕуNдЫЖЏЕФГѕЪМЮЛжУРыЕуOНќЃЌЙЪЕуQвЛжБЮЛгкЕуOгвВрЃЌгУOQМѕШЅ![]() MNЃЌЛЏМђМДПЩЕУНсТлЃЎ
MNЃЌЛЏМђМДПЩЕУНсТлЃЎ
НтЃКЃЈ1ЃЉЁпЃЈb+2ЃЉ2+ЃЈcЉ24ЃЉ2ЃН0ЃЌ
ЁрbЃНЉ2ЃЌcЃН24ЃЌ
ЁпЖрЯюЪНx|a+3|y2вЛax3y+xy2Љ1ЪЧЮхДЮЫФЯюЪНЃЌ
Ёр|a+3|ЃН5Љ2ЃЌЉaЁй0ЃЌ
ЁрaЃНЉ6ЃЛ
ЙЪД№АИЪЧЃКЉ6ЃЌЉ2ЃЌ24ЃЛ
ЃЈ2ЃЉЂйЕуPЃЌMЯргіЪБМфtЃН![]() ЃН7.5ЃЌ
ЃН7.5ЃЌ
ЁрNЕуЫљзпТЗГЬЃК7.5ЁС7ЃН52.5ЃЈЕЅЮЛГЄЖШЃЉЃЛ
ЂкOQЉ![]() MNЕФжЕВЛЗЂЩњБфЛЏЃЛРэгЩШчЯТЃК
MNЕФжЕВЛЗЂЩњБфЛЏЃЛРэгЩШчЯТЃК
ЩшдЫЖЏЕФЪБМфЮЊtУыЃЌ
дђMNЃНЃЈ7Љ1ЃЉt+4ЃН6t+4ЃЌ
ЁпЖЏЕуMЁЂNЁЂPЃЌЗжБ№ДгЕуAЁЂBЁЂCПЊЪМЭЌЪБГіЗЂдкЪ§жсЩЯдЫЖЏЃЌBЁЂCдкЪ§жсЩЯБэЪОЕФЪ§ЗжБ№ЮЊЉ2ЃЌ24ЃЌ
ЁрдЫЖЏtУыЪБЕуNЁЂPЗжБ№ЮЛгкЪ§жсЩЯЉ2+7tЁЂ24Љ3tЕФЮЛжУЃЌ
ЁрPNжаЕуQЮЛгкЃКЃЈЉ2+7t+24Љ3tЃЉЁТ2ЃН11+2tЃЌ
ЁрOQЃН11+2tЃЌ
ЁрOQЉ![]() MNЃН11+2tЉ
MNЃН11+2tЉ![]() ЃЈ6t+4ЃЉЃН11+2tЉ2tЉ
ЃЈ6t+4ЃЉЃН11+2tЉ2tЉ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрдкдЫЖЏЙ§ГЬжаЃЌOQЉ![]() MNЕФжЕВЛЗЂЩњБфЛЏЃЎ
MNЕФжЕВЛЗЂЩњБфЛЏЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌEЁЂFЁЂGЁЂHЗжБ№ЪЧBDЁЂBCЁЂACЁЂADЕФжаЕуЃЌЧвABЃНCDЃЎНсТлЃКЂйEGЁЭFHЃЛЂкЫФБпаЮEFGHЪЧОиаЮЃЛЂлHFЦНЗжЁЯEHGЃЛЂмEG![]() BCЃЛЂнЫФБпаЮEFGHЕФжмГЄЕШгк2ABЃЎЦфжае§ШЗЕФИіЪ§ЪЧ( )
BCЃЛЂнЫФБпаЮEFGHЕФжмГЄЕШгк2ABЃЎЦфжае§ШЗЕФИіЪ§ЪЧ( )
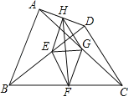
A. 1B. 2C. 3D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГДѓаЭГЌЪаДгЩњВњЛљЕиЙКНјвЛХњЫЎЙћЃЌдЫЪфЙ§ГЬжажЪСПЫ№ЪЇ5%ЃЌМйЩшВЛМЦГЌЪаЦфЫћЗбгУЃЎ
ЃЈ1ЃЉШчЙћГЌЪадкНјМлЕФЛљДЁЩЯЬсИп5%зїЮЊЪлМлЃЌФЧУДЧыФуЭЈЙ§МЦЫуЫЕУїГЌЪаЪЧЗёПїБОЃЛ
ЃЈ2ЃЉШчЙћГЌЪажСЩйвЊЛёЕУ20%ЕФРћШѓЃЌФЧУДетжжЫЎЙћЕФЪлМлзюЕЭгІЬсИпАйЗжжЎМИЃПЃЈНсЙћОЋШЗЕН0.1%ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛМмЗНЬнABГЄ25УзЃЌШчЭМЫљЪОЃЌаБППдквЛУцЩЯЃК

ЃЈ1ЃЉШєЬнзгЕзЖЫРыЧН7УзЃЌетИіЬнзгЕФЖЅЖЫОрЕиУцгаЖрИпЃП
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌШчЙћЬнзгЕФЖЅЖЫЯТЛЌСЫ4УзЃЌФЧУДЬнзгЕФЕзЖЫдкЫЎЦНЗНЯђЛЌЖЏСЫМИУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bx+cгыxжсНЛгкЕуAКЭBЃЈ1ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЌжБЯпy=![]() xЉ2ОЙ§AЃЌCСНЕуЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЎ
xЉ2ОЙ§AЃЌCСНЕуЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНКЭЖЅЕуDЕФзјБъЃЛ
ЃЈ2ЃЉдкyжсЩЯЪЧЗёДцдквЛЕуGЃЌЪЙЕУGD+GBЕФжЕзюаЁЃПШєДцдкЃЌЧѓГіЕуGЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїPABЪЧвдABЮЊбќЕФЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіPЕузјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТСаЫуЪНЃЌФуЗЂЯжСЫЪВУДЙцТЩЃП
12=![]() ЃЛ12+22=
ЃЛ12+22=![]() ЃЛ12+22+32 =
ЃЛ12+22+32 =![]() ЃЛ 12+22 +32 + 42 =
ЃЛ 12+22 +32 + 42 =![]() ЃЛЁ
ЃЛЁ
1ЃЉФуФмгУвЛИіЫуЪНБэЪОетИіЙцТЩТ№ЃП
2ЃЉИљОнФуЗЂЯжЕФЙцТЩЃЌМЦЫуЯТУцЫуЪНЕФжЕЃЛ
12+22 +32 + Ё +82
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁїABCЕФШ§ИіЖЅЕузјБъЗжБ№ЮЊAЃЈЉ2ЃЌ1ЃЉЃЌBЃЈЉ1ЃЌ4ЃЉЃЌCЃЈЉ3ЃЌ3ЃЉЃЎ
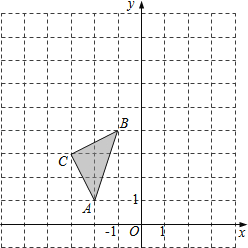
ЃЈ1ЃЉЛГіЁїABCЙигкyжсЖдГЦЕФЁїA1B1C1ЃЌВЂаДГіA1ЕуЕФзјБъМАsinЁЯB1A1C1ЕФжЕЃЛ
ЃЈ2ЃЉвддЕуOЮЊЮЛЫЦжааФЃЌЮЛЫЦБШЮЊ1ЃК2ЃЌдкyжсЕФзѓВрЃЌЛГі НЋЁїABCЗХДѓКѓЕФЁїA2B2C2ЃЌВЂаДГіA2ЕуЕФзјБъЃЛ
ЃЈ3ЃЉШєЕуDЃЈaЃЌbЃЉдкЯпЖЮABЩЯЃЌжБНгаДГіОЙ§ЃЈ2ЃЉЕФБфЛЏКѓЕуDЕФЖдгІЕуD2ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌACЃЌBDЯрНЛгкЕуOЃЌЕуEдкBCЩЯЃЌAEНЛBDгкFЃЎ
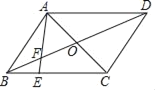
ЃЈ1ЃЉШєEЪЧППНќЕуBЕФШ§ЕШЗжЕуЃЌЧѓЃЛЂй![]() ЕФжЕЃЛЂкЁїBEFгыЁїDAFЕФУцЛ§БШЃЛ
ЕФжЕЃЛЂкЁїBEFгыЁїDAFЕФУцЛ§БШЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЪ§жсЩЯЕуAЃЌBЗжБ№ЖдгІЪ§aЃЌbЃЎЦфжаaЃМ0ЃЌbЃО0ЃЎ
ЃЈ1ЃЉЕБaЃНЉ2ЃЌbЃН6ЪБЃЌЯпЖЮABЕФжаЕуЖдгІЕФЪ§ЪЧЁЁ ЁЁЃЛЃЈжБНгЬюНсЙћЃЉ
ЃЈ2ЃЉШєИУЪ§жсЩЯСэгавЛЕуMЖдгІзХЪ§mЃЎ
ЂйЕБmЃН2ЃЌbЃО2ЃЌЧвAMЃН2BMЪБЃЌЧѓДњЪ§ЪНa+2b+20ЕФжЕЃЛ
ЂкЕБaЃНЉ2ЃЌЧвAMЃН3BMЪБЃЌаЁАВбнЫуЗЂЯжДњЪ§ЪН3bЉ4mЪЧвЛИіЖЈжЕЃЎ
РЯЪІЕуЦРЃКФуЕФбнЫуЗЂЯжЛЙВЛЭъећ!
ЧыЭЈЙ§бнЫуНтЪЭЃКЮЊЪВУДЁАаЁАВЕФбнЫуЗЂЯжЁБЪЧВЛЭъећЕФЃП
![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com