
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和B(1,0),与y轴交于点C,直线y=![]() x﹣2经过A,C两点,抛物线的顶点为D.
x﹣2经过A,C两点,抛物线的顶点为D.
(1)求抛物线的解析式和顶点D的坐标;
(2)在y轴上是否存在一点G,使得GD+GB的值最小?若存在,求出点G的坐标;若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在点P,使△PAB是以AB为腰的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由.

【答案】(1)y=﹣![]() x2+
x2+![]() x﹣2;D(
x﹣2;D(![]() ,
, ![]() );(2)G(0,
);(2)G(0, ![]() ),(3)P点坐标为(
),(3)P点坐标为(![]() ,
, ![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
【解析】试题分析:(1)先由直线y=![]() x﹣2与x轴的交点求出A点和C点的坐标,再用待定系数法求出求抛物线解析式即可;
x﹣2与x轴的交点求出A点和C点的坐标,再用待定系数法求出求抛物线解析式即可;
(2)作点B关于y轴的对称点B',连接BB',交y轴于点G,则B'(﹣1,0),用待定系数法求出直线B'D的解析式,再求与y轴的交点坐标即可;
(3)分AP=AB和BP=AB=3两种情况求解.
解:(1)把x=0代入直线y=![]() x﹣2中,y=﹣2,
x﹣2中,y=﹣2,
∴C(0,﹣2),
把y=0代入直线y=![]() x﹣2中,x=4,
x﹣2中,x=4,
∴A(4,0),
把A(4,0),B(1,0),C(0,﹣2)代入抛物线y=ax2+bx+c中得:
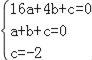 ,解得:
,解得:![]() ,
,
∴抛物线的解析式为:y=﹣![]() x2+
x2+![]() x﹣2=﹣
x﹣2=﹣![]() (x2﹣5x+
(x2﹣5x+![]() ﹣
﹣![]() )﹣2=﹣
)﹣2=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴顶点D(![]() ,
,![]() ),
),
(2)存在,
如图1,作点B关于y轴的对称点B',连接BB',交y轴于点G,则B'(﹣1,0),
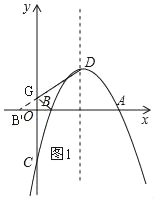
设直线B'D的解析式为:y=kx+b,
则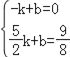 ,解得:
,解得:![]() ,
,
∴直线B'D的解析式为:y=![]() x+
x+![]() ,
,
∴G(0,![]() ),
),
∴存在点G(0,![]() ),使得GD+GB的值最小;
),使得GD+GB的值最小;
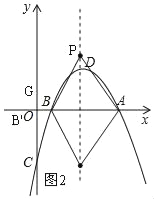
(3)∵对称轴x=![]() ,且A(4,0),B(1,0),
,且A(4,0),B(1,0),
设P(![]() ,m),且AB=4﹣1=3,
,m),且AB=4﹣1=3,
分两种情况:
①当AP=AB=3时,即AP=![]() =3,
=3,
解得:m=±![]() ,
,
②当BP=AB=3时,即BP=![]() =3,
=3,
解得:m=![]() ,
,
综上所述,P点坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:“熟练工人每月工资至少3800元.每天工作8小时,一个月工作25天.月工资底薪1000元,另加计件工资,且加工1件A型服装计酬20元,加工1件B型服装计酬15元”. (工人月工资=底薪+计件工资)在实际工作中发现一名熟练工加工1件A型服装的时间是加工1件B型服装的2倍,且工作5天(即40小时)单独加工B服装的件数比单独加工A服装的件数多20件.
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)探索规律观察下面由※组成的图案和算式,解答问题

(1)请计算1+3+5+7+9+11=__________;
(2)请猜想1+3+5+7+9+…+19=__________;
(3)请猜想1+3+5+7+9+…+(2n﹣1)=__________;
(4)请用上述规律计算:21+23+25+…+99.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②CB平分∠ABD;③∠AOC=∠AEC;④AF=DF;⑤BD=2OF.其中正确的结论有( )
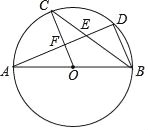
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
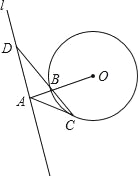
【题目】如图,直线l与⊙O相离,OA⊥l于点A,交⊙O于点B,点C是⊙O上一点,连接CB并延长交直线l于点D,使AC=AD.
(1)求证:AC是⊙O的切线;
(2)若BD=2![]() ,OA=4,求线段BC的长.
,OA=4,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B、C在数轴上表示的数分别为a,b,c,且a,b,c满足(b+2)2+(c﹣24)2=0,多项式x|a+3|y2﹣ax3y+xy2﹣1是五次四项式.
(1)a的值为 ,b的值为 ,c的值为 ;
(2)若数轴上有三个动点M、N、P,分别从点A、B、C开始同时出发在数轴上运动,速度分别为每秒1个单位长度、7个单位长度3个单位长度.
①若点P向左运动,点M向右运动,点N先向左运动,遇到点M后回头再向右运动,遇到点P后又回头再向左运动,……,这样直到点P遇到点M时三点都停止运动,求点N所走的路程;
②若点M、N向右运动,点P向左运动,点Q为线段PN中点,在运动过程中,OQ﹣![]() MN的值是否发生变化?若不变,求其值;若变化,说明理由.
MN的值是否发生变化?若不变,求其值;若变化,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子![]() (x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是
(x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是![]() ,矩形的周长是2(
,矩形的周长是2(![]() );当矩形成为正方形时,就有x=
);当矩形成为正方形时,就有x=![]() (x>0),解得x=1,这时矩形的周长2(
(x>0),解得x=1,这时矩形的周长2(![]() )=4最小,因此
)=4最小,因此![]() (x>0)的最小值是2.模仿张华的推导,你求得式子
(x>0)的最小值是2.模仿张华的推导,你求得式子![]() (x>0)的最小值是( )
(x>0)的最小值是( )
A. 2 B. 1 C. 6 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了奖励优秀班集体,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元,购买3幅乒乓球拍和2幅羽毛球拍共需204元.
(1)每副乒乓球拍和羽毛球拍的单价各是多少元?
(2)若学校购买5副乒乓球拍和3副羽毛球拍,一共应支出多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
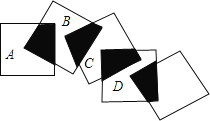
A.2cm2 B.4cm2 C.6cm2 D.8cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com