
ЁОЬтФПЁПеХЛЊдквЛДЮЪ§бЇЛюЖЏжаЃЌРћгУЁАдкУцЛ§вЛЖЈЕФОиаЮжаЃЌе§ЗНаЮЕФжмГЄзюЖЬЁБЕФНсТлЃЌЭЦЕМГіЁАЪНзг![]() ЃЈxЃО0ЃЉЕФзюаЁжЕЪЧ2ЁБЃЎЦфЭЦЕМЗНЗЈШчЯТЃКдкУцЛ§ЪЧ1ЕФОиаЮжаЩшОиаЮЕФвЛБпГЄЮЊxЃЌдђСэвЛБпГЄЪЧ
ЃЈxЃО0ЃЉЕФзюаЁжЕЪЧ2ЁБЃЎЦфЭЦЕМЗНЗЈШчЯТЃКдкУцЛ§ЪЧ1ЕФОиаЮжаЩшОиаЮЕФвЛБпГЄЮЊxЃЌдђСэвЛБпГЄЪЧ![]() ЃЌОиаЮЕФжмГЄЪЧ2ЃЈ
ЃЌОиаЮЕФжмГЄЪЧ2ЃЈ![]() ЃЉЃЛЕБОиаЮГЩЮЊе§ЗНаЮЪБЃЌОЭгаx=
ЃЉЃЛЕБОиаЮГЩЮЊе§ЗНаЮЪБЃЌОЭгаx=![]() ЃЈxЃО0ЃЉЃЌНтЕУx=1ЃЌетЪБОиаЮЕФжмГЄ2ЃЈ
ЃЈxЃО0ЃЉЃЌНтЕУx=1ЃЌетЪБОиаЮЕФжмГЄ2ЃЈ![]() ЃЉ=4зюаЁЃЌвђДЫ
ЃЉ=4зюаЁЃЌвђДЫ![]() ЃЈxЃО0ЃЉЕФзюаЁжЕЪЧ2ЃЎФЃЗТеХЛЊЕФЭЦЕМЃЌФуЧѓЕУЪНзг
ЃЈxЃО0ЃЉЕФзюаЁжЕЪЧ2ЃЎФЃЗТеХЛЊЕФЭЦЕМЃЌФуЧѓЕУЪНзг![]() ЃЈxЃО0ЃЉЕФзюаЁжЕЪЧЃЈ ЃЉ
ЃЈxЃО0ЃЉЕФзюаЁжЕЪЧЃЈ ЃЉ
A. 2 B. 1 C. 6 D. 10
 БИеНжаПМКЎМйЯЕСаД№АИ
БИеНжаПМКЎМйЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
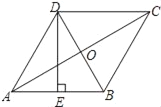
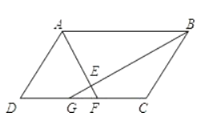
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌACЃЌBDЯрНЛгкЕуOЃЌEЮЊABЕФжаЕуЃЌDEЁЭABЃЎ
ЃЈ1ЃЉЧѓЁЯABCЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШчЙћAC=![]() ЃЌЧѓDEЕФГЄЃЎ
ЃЌЧѓDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖрЯюЪН![]() гыЖрЯюЪН
гыЖрЯюЪН![]() ЕФКЭжаВЛКЌга
ЕФКЭжаВЛКЌга![]() Яю
Яю
ЃЈ1ЃЉ![]() _____ЃЌ
_____ЃЌ![]() _____.
_____.
ЃЈ2ЃЉМЦЫуЃК![]() КЭ
КЭ![]() ЕФжЕЃЌВЂЭЈЙ§МЦЫуЕФНсЙћЃЌВТЯы
ЕФжЕЃЌВЂЭЈЙ§МЦЫуЕФНсЙћЃЌВТЯы![]() КЭ
КЭ![]() ЕФЙиЯЕ.
ЕФЙиЯЕ.
ЃЈ3ЃЉЧыФуРћгУВТЯыМЦЫуЃК![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bx+cгыxжсНЛгкЕуAКЭBЃЈ1ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЌжБЯпy=![]() xЉ2ОЙ§AЃЌCСНЕуЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЎ
xЉ2ОЙ§AЃЌCСНЕуЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНКЭЖЅЕуDЕФзјБъЃЛ
ЃЈ2ЃЉдкyжсЩЯЪЧЗёДцдквЛЕуGЃЌЪЙЕУGD+GBЕФжЕзюаЁЃПШєДцдкЃЌЧѓГіЕуGЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїPABЪЧвдABЮЊбќЕФЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіPЕузјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
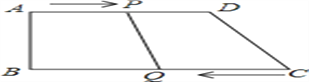
ЁОЬтФПЁПШчЭМ,дкЫФБпаЮABCDжа,ADЁЮBC, ЁЯBЉ90Ёу,ABЉ8ЉM,ADЉ24ЉM,BCЉ26ЉM,ЕуpДгЕуAГіЗЂ,вд1ЉM/sЕФЫйЖШЯђЕуDдЫЖЏ;ЕуQДгЕуCЭЌЪБГіЗЂ,вд3ЉM/sЕФЫйЖШЯђЕуBдЫЖЏ,ЙцЖЈЦфжавЛИіЖЏЕуЕНДяЖЫЕуЪБ,СэвЛИіЖЏЕувВЫцжЎЭЃжЙдЫЖЏ. ЩшдЫЖЏЪБМфЮЊt s.
ЃЈ1ЃЉtЮЊКЮжЕЪБ,ЫФБпаЮPQCDЮЊЦНааЫФБпаЮ?
ЃЈ2ЃЉtЮЊКЮжЕЪБ,ЫФБпаЮPQCDЮЊЕШбќЬнаЮ?ЃЈЕШбќЬнаЮЕФСНбќЯрЕШЃЌСНЕзНЧЯрЕШЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁїABCЕФШ§ИіЖЅЕузјБъЗжБ№ЮЊAЃЈЉ2ЃЌ1ЃЉЃЌBЃЈЉ1ЃЌ4ЃЉЃЌCЃЈЉ3ЃЌ3ЃЉЃЎ
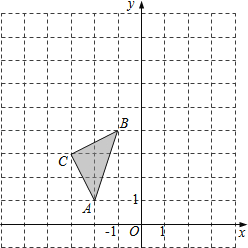
ЃЈ1ЃЉЛГіЁїABCЙигкyжсЖдГЦЕФЁїA1B1C1ЃЌВЂаДГіA1ЕуЕФзјБъМАsinЁЯB1A1C1ЕФжЕЃЛ
ЃЈ2ЃЉвддЕуOЮЊЮЛЫЦжааФЃЌЮЛЫЦБШЮЊ1ЃК2ЃЌдкyжсЕФзѓВрЃЌЛГі НЋЁїABCЗХДѓКѓЕФЁїA2B2C2ЃЌВЂаДГіA2ЕуЕФзјБъЃЛ
ЃЈ3ЃЉШєЕуDЃЈaЃЌbЃЉдкЯпЖЮABЩЯЃЌжБНгаДГіОЙ§ЃЈ2ЃЉЕФБфЛЏКѓЕуDЕФЖдгІЕуD2ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
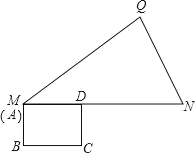
ЁОЬтФПЁПШчЭМЃЌдкЁїMNQжаЃЌMN=11ЃЌNQ=![]() ЃЌ
ЃЌ![]() ЃЌОиаЮABCDЃЌBC=4ЃЌCD=3ЃЌЕуAгыMжиКЯЃЌADгыMNжиКЯЃЎОиаЮABCDбизХMQЗНЯђЦНвЦЃЌЧвЦНвЦЫйЖШЮЊУПУы5ИіЕЅЮЛЃЌЕБЕуAгыQжиКЯЪБЭЃжЙдЫЖЏЃЎ
ЃЌОиаЮABCDЃЌBC=4ЃЌCD=3ЃЌЕуAгыMжиКЯЃЌADгыMNжиКЯЃЎОиаЮABCDбизХMQЗНЯђЦНвЦЃЌЧвЦНвЦЫйЖШЮЊУПУы5ИіЕЅЮЛЃЌЕБЕуAгыQжиКЯЪБЭЃжЙдЫЖЏЃЎ
ЃЈ1ЃЉMQЕФГЄЖШЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉдЫЖЏЁЁ ЁЁУыЃЌBCгыMNжиКЯЃЛ
ЃЈ3ЃЉЩшОиаЮABCDгыЁїMNQжиЕўВПЗжЕФУцЛ§ЮЊSЃЌдЫЖЏЪБМфЮЊtЃЌЧѓГіSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНсКЯЪ§жсгыОјЖджЕЕФжЊЪЖЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЪ§жсЩЯБэЪО4КЭ1ЕФСНЕужЎМфЕФОрРыЪЧЁЁ ЁЁЃЛБэЪОЉ3КЭ2СНЕужЎМфЕФОрРыЪЧЁЁ ЁЁЃЛвЛАуЕиЃЌЪ§жсЩЯБэЪОЪ§mКЭЪ§nЕФСНЕужЎМфЕФОрРыЕШгк|mЉn|ЃЎШчЙћБэЪОЪ§aКЭЉ2ЕФСНЕужЎМфЕФОрРыЪЧ3ЃЌФЧУДaЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєЪ§жсЩЯБэЪОЪ§aЕФЕуЮЛгкЉ4гы2жЎМфЃЌЧѓ|a+4|+|aЉ2|ЕФжЕЃЛ
ЃЈ3ЃЉЕБaШЁКЮжЕЪБЃЌ|a+5|+|aЉ1|+|aЉ4|ЕФжЕзюаЁЃЌзюаЁжЕЪЧЖрЩйЃПЧыЫЕУїРэгЩЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮ ![]() жаЃЌ
жаЃЌ![]() ЁЂ
ЁЂ![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп ![]() ЗжБ№гыЯпЖЮ
ЗжБ№гыЯпЖЮ ![]() НЛгкЕу
НЛгкЕу ![]() ЃЌ
ЃЌ![]() гы
гы ![]() НЛгкЕу
НЛгкЕу ![]() ЃЎ
ЃЎ
(1) ЧѓжЄЃК![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
(2) Шє ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ ![]() КЭ
КЭ ![]() ЕФГЄЖШЃЎ
ЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com