
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD=( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD=( )| A. | 22.5° | B. | 30° | C. | 36° | D. | 45° |
分析 先求出∠BCD和∠ACD,再根据直角三角形两锐角互余求出∠B,根据直角三角形斜边上的中线等于斜边的一半可得CE=BE,根据等边对等角可得∠BCE=∠B,再求出∠ECD=45°.
解答 解:∵∠ACB=90°,∠ACD=3∠BCD,
∴∠BCD=90°×$\frac{1}{1+3}$=22.5°,
∠ACD=90°×$\frac{3}{1+3}$=67.5°,
∵CD⊥AB,
∴∠B=90°-22.5°=67.5°,
∵E是AB的中点,∠ACB=90°,
∴CE=BE,
∴∠BCE=∠B=67.5°,
∴∠ECD=∠BCE-∠BCD=67.5°-22.5°=45°,
故选D.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的性质,熟记性质并准确识图,理清图中各角度之间的关系是解题的关键.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
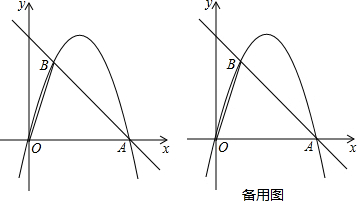
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
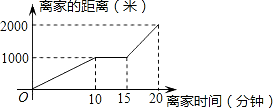 某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.图中描述了他上学的途中离家距离S(米)与离家时间t(分)之间的函数关系.下列说法中正确的个数是( )
某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.图中描述了他上学的途中离家距离S(米)与离家时间t(分)之间的函数关系.下列说法中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
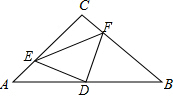 如图,在△ABC中,∠C=90°,CA=CB,D是AB的中点,点E、F在AB、AC边上运动(点E不与A、C重合),且保持AE=CF,连接DE,DF,EF.有下列结论:
如图,在△ABC中,∠C=90°,CA=CB,D是AB的中点,点E、F在AB、AC边上运动(点E不与A、C重合),且保持AE=CF,连接DE,DF,EF.有下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com