
科目:初中数学 来源: 题型:解答题
 如图所示,A、B是笔直公路l同侧的两个村庄,且两个村庄到公路l的距离分别是300m和500m,两村庄之间的距离为600m,现要在公路上建一汽车停靠站,使两村到停靠站的距离之和最小,问最小值是多少?
如图所示,A、B是笔直公路l同侧的两个村庄,且两个村庄到公路l的距离分别是300m和500m,两村庄之间的距离为600m,现要在公路上建一汽车停靠站,使两村到停靠站的距离之和最小,问最小值是多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
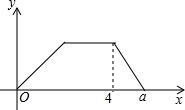 最近重庆八中学生宿舍在增修安全通道,一辆拉砖的货车从仓库匀速驶往学校,到达后用了1小时卸货,随即匀速返回.已知货车返回的速度是它从仓库驶往学饺的速度的2倍,货车离仓库的距离y(千米)关于时间x的函数图象如图所示.则a=4.5(小时).
最近重庆八中学生宿舍在增修安全通道,一辆拉砖的货车从仓库匀速驶往学校,到达后用了1小时卸货,随即匀速返回.已知货车返回的速度是它从仓库驶往学饺的速度的2倍,货车离仓库的距离y(千米)关于时间x的函数图象如图所示.则a=4.5(小时).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD=( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD=( )| A. | 22.5° | B. | 30° | C. | 36° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
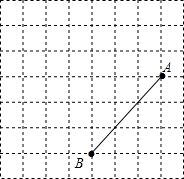 请在网格中建立平面直角坐标系,使得A点的坐标为(4,2).
请在网格中建立平面直角坐标系,使得A点的坐标为(4,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
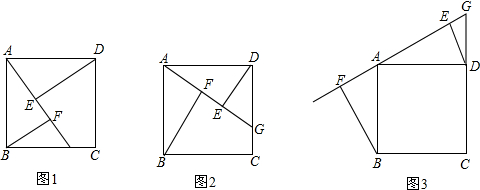
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com