
【题目】如图,![]() 的半径为2.弦
的半径为2.弦![]() ,点
,点![]() 为优弧
为优弧![]() 上一动点,
上一动点,![]() 交直线
交直线![]() 于点
于点![]() ,则
,则![]() 的最大面积是__________________.
的最大面积是__________________.
【答案】![]()
【解析】
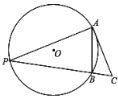
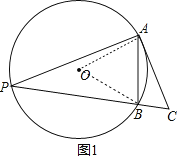
连结OA、OB,如图1,由OA=OB=AB=2可判断△OAB为等边三角形,则∠AOB=60°,根据圆周角定理得![]() ,由于AC⊥AP,所以∠C=60°,因为AB=2,则要使△ABC的最大面积,点C到AB的距离要最大;由∠ACB=60°,可根据圆周角定理判断点C在⊙D上,且∠ADB=120°,如图2,于是当点C优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,从而得到△ABC的最大面积.
,由于AC⊥AP,所以∠C=60°,因为AB=2,则要使△ABC的最大面积,点C到AB的距离要最大;由∠ACB=60°,可根据圆周角定理判断点C在⊙D上,且∠ADB=120°,如图2,于是当点C优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,从而得到△ABC的最大面积.
连结OA、OB,作△ABC的外接圆D,如图1,2
∵OA=OB=2,AB=2,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴![]() ,
,
∵AC⊥AP,
∴∠C=60°,
∵AB=2,要使△ABC的最大面积,则点C到AB的距离最大,
∵∠ACB=60°,点C在⊙D上,
∴∠ADB=120°,
如图2,
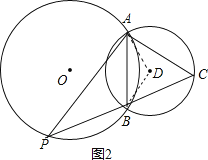
当点C为优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,且面积为![]() ,
,
∴△ABC的最大面积为![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。
(1)将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 为常数,
为常数,![]() ),其对称轴是
),其对称轴是![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() ,
,![]() 之间.有下列结论:①
之间.有下列结论:①![]() ;②
;②![]() ;③若此抛物线过
;③若此抛物线过![]() 和
和![]() 两点,则
两点,则![]() ,其中,正确结论的个数为( )
,其中,正确结论的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() ,
,![]() .
.
(1)求该抛物线的函数表达式及对称轴;
(2)设点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 是抛物线对称轴上一动点,记抛物线在
是抛物线对称轴上一动点,记抛物线在![]() ,
,![]() 之间的部分为图象
之间的部分为图象![]() (包含
(包含![]() ,
,![]() 两点),如果直线
两点),如果直线![]() 与图象
与图象![]() 有一个公共点,结合函数的图象,直接写出点
有一个公共点,结合函数的图象,直接写出点![]() 纵坐标
纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年疫情防控期间.某小区卫生所决定购买A,B两种口罩.以满足小区居民的需要.若购买A种口罩9包,B种口罩4包,则需要700元;若购买A种口罩3包.B种口罩5包.则需要380元.
(1)购买人A,B两种口罩每包各需名少元?
(2)卫生所准备购进这两种口罩共90包,并且A种口罩包数不少于B种口罩包数的2倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() .
.
(1)用含![]() 的式子表示
的式子表示![]() ;
;
(2)直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
(3)在(2)的条件下,已知点![]() ,若抛物线与线段
,若抛物线与线段![]() 恰有两个公共点,求
恰有两个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 分别与x轴,y轴交于点
分别与x轴,y轴交于点![]() ,点C是第一象限内的一点,且
,点C是第一象限内的一点,且![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点,与x轴的另一交点为D.
两点,与x轴的另一交点为D.
(1)求此抛物线的解析式;
(2)判断直线![]() 与
与![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以![]() 四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,有两个形状完全相同的直角三角形ABC和EFG叠放在一起(点A与点E重合),已知AC=8cm,BC=6cm,∠C=90°,EG=4cm,∠EGF=90°,O是△EFG斜边上的中点.
如图②,若整个△EFG从图①的位置出发,以1cm/s的速度沿射线AB方向平移,在△EFG平移的同时,点P从△EFG的顶点G出发,以1cm/s的速度在直角边GF上向点F运动,当点P到达点F时,点P停止运动,△EFG也随之停止平移.设运动时间为x(s),FG的延长线交AC于H,四边形OAHP的面积为y(cm2)(不考虑点P与G、F重合的情况).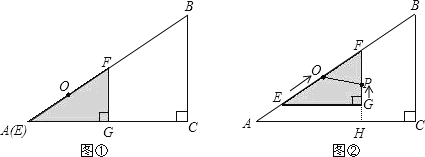
(1)当x为何值时,OP∥AC;
(2)求y与x之间的函数关系式,并确定自变量x的取值范围;
(3)是否存在某一时刻,使四边形OAHP面积与△ABC面积的比为13:24?若存在,求出x的值;若不存在,说明理由.(参考数据:1142=12996,1152=13225,1162=13456或4.42=19.36,4.52=20.25,4.62=21.16)
查看答案和解析>>
科目:初中数学 来源: 题型:
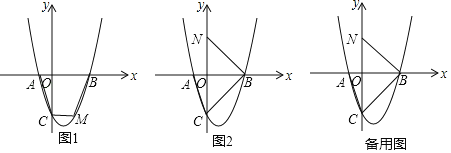
【题目】已知:如图,抛物线y=x2+bx+c与x轴相交于AB两点,与y轴相交于点C,若A(﹣1,0),且OC=3OA.
(1)填空:b= ,c= ;
(2)在图1中,若点M为抛物线上第四象限内一动点,顺次连接AC,CM,MB,求四边形ACMB面积的最大值;
(3)在图2中,将直线BC沿x轴翻折交y轴于点N,过点B的直线与抛物线相交于点D.若∠NBD=∠OCA,请直接写出点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com