
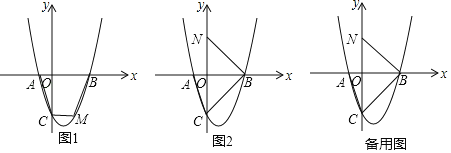
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌХзЮяЯпyЃНx2+bx+cгыxжсЯрНЛгкABСНЕуЃЌгыyжсЯрНЛгкЕуCЃЌШєAЃЈЉ1ЃЌ0ЃЉЃЌЧвOCЃН3OAЃЎ
ЃЈ1ЃЉЬюПеЃКbЃНЁЁ ЁЁЃЌcЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉдкЭМ1жаЃЌШєЕуMЮЊХзЮяЯпЩЯЕкЫФЯѓЯоФквЛЖЏЕуЃЌЫГДЮСЌНгACЃЌCMЃЌMBЃЌЧѓЫФБпаЮACMBУцЛ§ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉдкЭМ2жаЃЌНЋжБЯпBCбиxжсЗелНЛyжсгкЕуNЃЌЙ§ЕуBЕФжБЯпгыХзЮяЯпЯрНЛгкЕуDЃЎШєЁЯNBDЃНЁЯOCAЃЌЧыжБНгаДГіЕуDЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉЉ2ЃЌЉ3ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЕуDЕФзјБъЮЊЃЈЉ
ЃЛЃЈ3ЃЉЕуDЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈЉ3ЃЌ12ЃЉЃЎ
ЃЉЛђЃЈЉ3ЃЌ12ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩAЃЈ1ЃЌ0ЃЉгыOCЃН3OAЧѓЕуCзјБъЃЌАбЕуAЁЂCДњШыгУД§ЖЈЯЕЪ§ЗЈЧѓХзЮяЯпНтЮіЪНЃЌМДЧѓЕУbЁЂcЕФжЕЃЎ
ЃЈ2ЃЉСЌНгBCЃЌАбЫФБпаЮACMBЗжГЩЁїABCгыЁїBCMЃЎЧѓЕуBзјБъЃЌНјЖјЧѓЁїABCУцЛ§КЭжБЯпBCНтЮіЪНЃЎЩшЕуMКсзјБъЮЊmЃЌЙ§ЕуMзїMFЁЭxжсгкЕуFЃЌНЛBCгкЕуEЃЌгУmБэЪОEMЕФГЄЃЎАбЁїBCMЗжГЩЁїBEMгыЁїCEMЧѓУцЛ§КЭЃЌЕУЕНЙигкmЕФЖўДЮКЏЪ§ЙиЯЕЪНЃЌХфЗНМДЕУЕНЁїBCMУцЛ§зюДѓжЕЃЌНјЖјЧѓЕУЫФБпаЮACMBУцЛ§ЕФзюДѓжЕЃЎ
ЃЈ3ЃЉгЩOCЃН3OAЧѓЕУtanЁЯOCAЕФжЕЃЌЧѓЕуNзјБъКЭBNЕФГЄЃЎЙ§ЕуNзїGNЁЭBNЃЌИљОнЁЯNBDЃНЁЯOCAПЩЕУtanЁЯNBDЃН![]() ЃЌМДЧѓЕУNGЕФГЄЃЌНјЖјгУЙДЙЩЖЈРэЧѓЕУBNЕФГЄЃЎЩшЕуGзјБъЮЊЃЈsЃЌtЃЉЃЌгУsЁЂtБэЪОNG2ЃЌBG2ЕФжЕЃЌМДСаЕУЙигкsЁЂtЕФЗНГЬзщЃЌЧѓНтЕУСНИіТњзуЬѕМўЕФЕуGЃЎЧѓжБЯпBGНтЮіЪНЃЌгыХзЮяЯпНтЮіЪНСЊСЂЗНГЬзщМДЧѓЕУЕуDзјБъЃЎ
ЃЌМДЧѓЕУNGЕФГЄЃЌНјЖјгУЙДЙЩЖЈРэЧѓЕУBNЕФГЄЃЎЩшЕуGзјБъЮЊЃЈsЃЌtЃЉЃЌгУsЁЂtБэЪОNG2ЃЌBG2ЕФжЕЃЌМДСаЕУЙигкsЁЂtЕФЗНГЬзщЃЌЧѓНтЕУСНИіТњзуЬѕМўЕФЕуGЃЎЧѓжБЯпBGНтЮіЪНЃЌгыХзЮяЯпНтЮіЪНСЊСЂЗНГЬзщМДЧѓЕУЕуDзјБъЃЎ
НтЃКЃЈ1ЃЉЁпAЃЈЉ1ЃЌ0ЃЉ
ЁрOAЃН1
ЁрOCЃН3OAЃН3
ЁрCЃЈ0ЃЌЉ3ЃЉ
ЁпХзЮяЯпyЃНx2+bx+cОЙ§ЕуAЁЂC
Ёр![]() НтЕУЃК
НтЕУЃК![]()
ЙЪД№АИЮЊЃКЉ2ЃЌЉ3ЃЎ
ЃЈ2ЃЉШчЭМ1ЃЌСЌНгBCЃЌЙ§ЕуMзїMFЁЭxжсгкЕуFЃЌНЛBCгкЕуE
ЁпХзЮяЯпНтЮіЪНЮЊyЃНx2Љ2xЉ3
ЁрЕБx2Љ2xЉ3ЃН0ЪБЃЌНтЕУЃКx1ЃНЉ1ЃЌx2ЃН3
ЁрBЃЈ3ЃЌ0ЃЉЃЌABЃН3ЉЃЈЉ1ЃЉЃН4
ЁрSЁїABCЃН![]() ABOCЃН
ABOCЃН![]() ЁС4ЁС3ЃН6
ЁС4ЁС3ЃН6
ЩшжБЯпBCНтЮіЪНЮЊЃКyЃНkxЉ3
АбЕуBДњШыЕУЃК3kЉ3ЃН0ЃЌНтЕУЃКkЃН1
ЁржБЯпBCЃКyЃНxЉ3
ЁпЕуMЮЊХзЮяЯпЩЯЕкЫФЯѓЯоФкЕФЕу
ЁрЩшЕуMзјБъЮЊЃЈmЃЌm2Љ2mЉ3ЃЉЃЈ0ЃМmЃМ3ЃЉ
ЁрEЃЈmЃЌmЉ3ЃЉ
ЁрEMЃНmЉ3ЉЃЈm2Љ2mЉ3ЃЉЃНЉm2+3mЃНЉЃЈmЉ![]() ЃЉ2+
ЃЉ2+![]()
ЁрSЁїBCMЃНSЁїBEM+SЁїCEM
ЃН![]() EMBF+
EMBF+![]() EMOF
EMOF
ЃН![]() EMЃЈBF+OFЃЉ
EMЃЈBF+OFЃЉ
ЃН![]() EMOB
EMOB
ЃН![]() [ЉЃЈmЉ
[ЉЃЈmЉ![]() ЃЉ2+
ЃЉ2+![]() ]
]
ЃНЉ![]() ЃЈmЉ
ЃЈmЉ![]() ЃЉ2+
ЃЉ2+![]()
ЁрSЫФБпаЮACMBЃНSЁїABC+SЁїBCMЃН6Љ![]() ЃЈmЉ
ЃЈmЉ![]() ЃЉ2+
ЃЉ2+![]() ЃНЉ
ЃНЉ![]() ЃЈmЉ
ЃЈmЉ![]() ЃЉ2+
ЃЉ2+![]()
ЁрЫФБпаЮACMBУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЙ§ЕуNзїNGЁЭBNЃЌНЛжБЯпBDгкЕуG
ЁрЁЯBNGЃНЁЯAOCЃН90Ёу
ЁпOCЃН3OA
ЁрRtЁїAOCжаЃЌtanЁЯOCAЃН![]()
ЁпЁЯNBDЃНЁЯOCA
ЁрtanЁЯNBDЃНtanЁЯOCAЃН![]()
ЁрRtЁїBNGжаЃЌtanЁЯNBDЃН![]()
ЁпBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ3ЃЉЃЌНЋжБЯпBCбиxжсЗелНЛyжсгкЕуN
ЁрNЃЈ0ЃЌ3ЃЉ
ЁрBNЃН![]()
ЁрNGЃН![]() BNЃН
BNЃН![]()
ЁрBGЃН![]()
ЩшЕуGзјБъЮЊЃЈsЃЌtЃЉ
ЁрNG2ЃНs2+ЃЈtЉ3ЃЉ2ЃЌBG2ЃНЃЈ3ЉsЃЉ2+t2
Ёр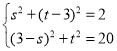 НтЕУЃК
НтЕУЃК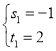 ,
,![]()
ЁрЕуGзјБъЮЊЃЈЉ1ЃЌ2ЃЉЛђЃЈ1ЃЌ4ЃЉ
ЂйGЃЈЉ1ЃЌ2ЃЉЃЌЩшжБЯпBGНтЮіЪНЮЊyЃНax+g
Ёр![]() НтЕУЃК
НтЕУЃК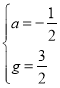
ЁржБЯпBGЃКyЃНЉ![]() x+
x+![]()
Ёп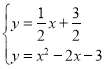 НтЕУЃК
НтЕУЃК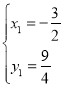 ,
,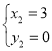 ЃЈМДЕуBЃЉ
ЃЈМДЕуBЃЉ
ЁрDЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЂкGЃЈ1ЃЌ4ЃЉЃЌЩшЩшжБЯпBGНтЮіЪНЮЊyЃНpx+q
Ёр![]() НтЕУЃК
НтЕУЃК![]()
ЁржБЯпBGЃКyЃН-2x+6
Ёп![]() НтЕУЃК
НтЕУЃК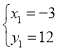 ,
,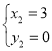 ЃЈМДЕуBЃЉ
ЃЈМДЕуBЃЉ
ЁрD ЃЈЉ3ЃЌ12ЃЉ
злЩЯЫљЪіЃЌШєЁЯNBDЃНЁЯOCA/span>ЃЌЕуDЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈЉ3ЃЌ12ЃЉЃЎ
ЃЉЛђЃЈЉ3ЃЌ12ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЕФАыОЖЮЊ2ЃЎЯв
ЕФАыОЖЮЊ2ЃЎЯв![]() ЃЌЕу
ЃЌЕу![]() ЮЊгХЛЁ
ЮЊгХЛЁ![]() ЩЯвЛЖЏЕуЃЌ
ЩЯвЛЖЏЕуЃЌ![]() НЛжБЯп
НЛжБЯп![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ЕФзюДѓУцЛ§ЪЧ__________________ЃЎ
ЕФзюДѓУцЛ§ЪЧ__________________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() ЁЂ
ЁЂ![]() ЯђЙ§Еу
ЯђЙ§Еу![]() ЕФжБЯпзїДЙЯпЃЌДЙзуЗжБ№ЮЊ
ЕФжБЯпзїДЙЯпЃЌДЙзуЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЭМЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
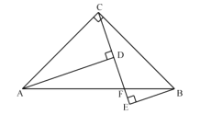
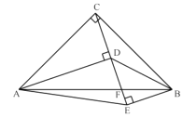
ЃЈ2ЃЉШчЭМЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌШє
ЃЌШє![]() ЃЌдкВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌЧыжБНгаДГіЫФИіНЧЃЌЪЙаДГіЕФУПвЛИіНЧЕФе§ЧажЕЖМЕШгк
ЃЌдкВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌЧыжБНгаДГіЫФИіНЧЃЌЪЙаДГіЕФУПвЛИіНЧЕФе§ЧажЕЖМЕШгк![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
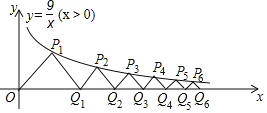
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуP1ЃЈx1ЃЌy1ЃЉЁЂP2ЃЈx2ЃЌy2ЃЉЁЂP3ЃЈx3ЃЌy3ЃЉЃЌЁЁЃЌPnЃЈxnЃЌynЃЉОљдкЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌЕуQ1ЁЂQ2ЁЂQ3ЁЂЁЁЁЂQnОљдкxжсЕФе§АыжсЩЯЃЌЧвЁїOP1Q1ЁЂЁїQ1P2Q2ЁЂЁїQ2P3Q3ЁЂЁЁЂЁїQnЉ1PnQnОљЮЊЕШбќжБНЧШ§НЧаЮЃЌOQ1ЁЂQ1Q2ЁЂQ2Q3ЁЂЁЁЁЂQnЉ1QnЗжБ№ЮЊвдЩЯЕШбќжБНЧШ§НЧаЮЕФЕзБпЃЌдђy1+y2+y3+Ё+y2019ЕФжЕЕШгк_____ЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌЕуQ1ЁЂQ2ЁЂQ3ЁЂЁЁЁЂQnОљдкxжсЕФе§АыжсЩЯЃЌЧвЁїOP1Q1ЁЂЁїQ1P2Q2ЁЂЁїQ2P3Q3ЁЂЁЁЂЁїQnЉ1PnQnОљЮЊЕШбќжБНЧШ§НЧаЮЃЌOQ1ЁЂQ1Q2ЁЂQ2Q3ЁЂЁЁЁЂQnЉ1QnЗжБ№ЮЊвдЩЯЕШбќжБНЧШ§НЧаЮЕФЕзБпЃЌдђy1+y2+y3+Ё+y2019ЕФжЕЕШгк_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаЙњЙХДњгаШєЛдЛЭЕФЪ§бЇГЩОЭЃЌЁЖжмїТЫуОЁЗЃЌЁЖОХеТЫуЪѕЁЗЃЌЁЖКЃЕКЫуОЁЗЃЈЗжБ№гУзжФИAЁЂBЁЂCвРДЮБэЪОетШ§ВПзЈжјЃЉЕШЪЧЮвЙњЙХДњЪ§бЇЕФживЊЮФЯзЃЎНЋAЁЂBЁЂCетШ§ИізжФИЗжБ№аДдк3еХЭъШЋЯрЭЌЕФВЛЭИУїПЈЦЌЕФе§УцЩЯЃЌАбет3еХПЈЦЌБГУцГЏЩЯЯДОљКѓЗХдкзРУцЩЯаЁУїЯШДгжаЫцЛњГщШЁеХПЈЦЌЃЌМЧТМЯТПЈЦЌЩЯЕФзжФИЃЌЗХЛиКѓЯДОљЃЌдйгЩаЁЧПДгжаЫцЛњГщШЁеХПЈЦЌЃЌЧыгУСаБэЗЈЛђЛЪїзДЭМЗЈЃЌЧѓаЁУїКЭаЁЧПГщЕНЕФПЈЦЌЩЯЕФзжФИЯрЭЌЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌвд
ЕФжаЕуЃЌвд![]() ЮЊжБОЖзі
ЮЊжБОЖзі![]() ЗжБ№НЛ
ЗжБ№НЛ![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉЧѓжЄЃК![]() .
.
ЃЈ2ЃЉШчЭМ2ЃЌСЌ![]() ЃЌ
ЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЧѓжЄЃКЫФБпаЮ
ЪБЃЌЧѓжЄЃКЫФБпаЮ![]() ЪЧСтаЮ.
ЪЧСтаЮ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕШбќШ§НЧаЮ![]() жаЃЌ
жаЃЌ![]() ЪЧ
ЪЧ![]() ЕФНЧЦНЗжЯпЃЌЕу
ЕФНЧЦНЗжЯпЃЌЕу![]() дкЩфЯп
дкЩфЯп![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌШє
ЃЌШє![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЕФГЄЖШЮЊ_______ЃЎ
ЕФГЄЖШЮЊ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
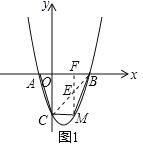
ЁОЬтФПЁПШчЭМЃЌОиаЮOABCдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊзјБъдЕуЃЌЕуAЃЈ0ЃЌ4ЃЉЃЌCЃЈ2ЃЌ0ЃЉЃЌНЋОиаЮOABCШЦЕуOАДЫГЪБеыЗНЯђа§зЊ1350ЃЌЕУЕНОиаЮEFGHЃЈЕуEгыOжиКЯЃЉ.
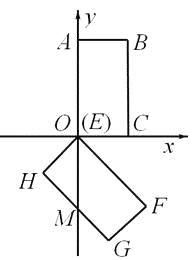
ЃЈ1ЃЉШєGHНЛyжсгкЕуMЃЌдђЁЯFOMЃН ЃЌOM= ЃЛ
ЃЈ2ЃЉОиаЮEFGHбиyжсЯђЩЯЦНвЦtИіЕЅЮЛ.
ЂйжБЯпGHгыxжсНЛгкЕуDЃЌШєADЁЮBOЃЌЧѓtЕФжЕЃЛ
ЂкШєОиаЮEFHGгыОиаЮOABCжиЕўВПЗжЕФУцЛ§ЮЊSИіЦНЗНЕЅЮЛЃЌЪдЧѓЕБ0<tЁм![]() ЪБЃЌSгыtжЎМфЕФКЏЪ§ЙиЯЕЪН.
ЪБЃЌSгыtжЎМфЕФКЏЪ§ЙиЯЕЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
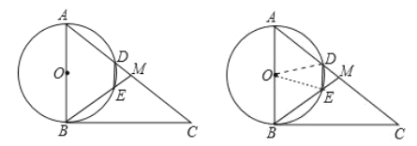
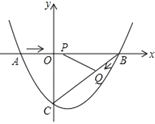
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЁЂ
ЁЂ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕу![]() Дг
Дг![]() ЕуГіЗЂЃЌдкЯпЖЮ
ЕуГіЗЂЃЌдкЯпЖЮ![]() ЩЯвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШЯђ
ЩЯвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШЯђ![]() ЕудЫЖЏЃЌЭЌЪБЕу
ЕудЫЖЏЃЌЭЌЪБЕу![]() Дг
Дг![]() ЕуГіЗЂЃЌдкЯпЖЮ
ЕуГіЗЂЃЌдкЯпЖЮ![]() ЩЯвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђ
ЩЯвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђ![]() ЕудЫЖЏЃЌЦфжавЛИіЕуЕНДяжеЕуЪБЃЌСэвЛИіЕувВЭЃжЙдЫЖЏЃЌЕБ
ЕудЫЖЏЃЌЦфжавЛИіЕуЕНДяжеЕуЪБЃЌСэвЛИіЕувВЭЃжЙдЫЖЏЃЌЕБ![]() ДцдкЪБЃЌЧѓдЫЖЏЖрЩйУыЪЙ
ДцдкЪБЃЌЧѓдЫЖЏЖрЩйУыЪЙ![]() ЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧЖрЩйЃП
ЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com