
【题目】已知抛物线![]() (
(![]() 为常数,
为常数,![]() ),其对称轴是
),其对称轴是![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() ,
,![]() 之间.有下列结论:①
之间.有下列结论:①![]() ;②
;②![]() ;③若此抛物线过
;③若此抛物线过![]() 和
和![]() 两点,则
两点,则![]() ,其中,正确结论的个数为( )
,其中,正确结论的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
逐一分析3条结论是否正确:①根据抛物线的对称轴为x=1,即可得出b=-2a![]() ,再根据抛物线开口方向和对称性,结合已知抛物线与
,再根据抛物线开口方向和对称性,结合已知抛物线与![]() 轴的一个交点在
轴的一个交点在![]() ,
,![]() 之间,可得抛物线与
之间,可得抛物线与![]() 轴的另一个交点在
轴的另一个交点在![]() ,
,![]() 之间,由此可得抛物线与y轴的正半轴相交,即可得出①正确;②由①可知抛物线开口向下,与
之间,由此可得抛物线与y轴的正半轴相交,即可得出①正确;②由①可知抛物线开口向下,与![]() 轴的另一个交点在
轴的另一个交点在![]() ,
,![]() 之间,当x=-1时,的函数值小于0,即可得出②错误;③根据抛物线的对称性可得
之间,当x=-1时,的函数值小于0,即可得出②错误;③根据抛物线的对称性可得![]() 与(4,
与(4,![]() )关于对称轴对称,再根据抛物线的增减性得出③正确;综上即可得出结论.
)关于对称轴对称,再根据抛物线的增减性得出③正确;综上即可得出结论.
解:∵抛物线的对称轴为x=1,
∴![]() ,∵
,∵![]()
∴![]()
∵抛物线与x轴的正半轴交点在点(2,0)和(3,0)之间,对称轴是x=1,
∴抛物线与x轴的另一个交点在点(0,0)和点(-1,0)之间,
∴抛物线与y轴的正半轴相交,∴![]()
∴![]() ,①正确;
,①正确;
∵抛物线与x轴的另一个交点在点(0,0)和点(-1,0)之间,
∴当x=-1时,y=a-b+c<0,故②错误;,
∵抛物线的对称轴为x=1,
∴![]() 与(4,
与(4,![]() )关于对称轴对称,
)关于对称轴对称,
∵抛物线开口向下,当x![]() 时,y随x的增大而减小,
时,y随x的增大而减小,
∴![]() ,故③正确,
,故③正确,
故选:C.


科目:初中数学 来源: 题型:
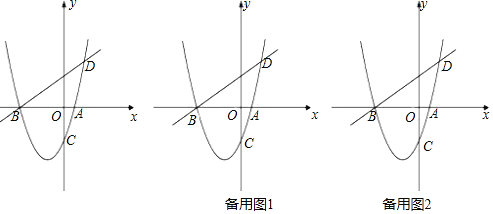
【题目】如图,已知抛物线![]() 与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且
与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C,求![]() 面积的最大值;
面积的最大值;
(3)在(2)中![]() 面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣6mx+9m+1(m≠0).
(1)求抛物线的顶点坐标;
(2)若抛物线与x轴的两个交点分别为A和B点(点A在点B的左侧),且AB=4,求m的值.
(3)已知四个点C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若抛物线与线段CD和线段EF都没有公共点,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一天,水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克,后再到水果市场去卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:
品名 | 猕猴桃 | 芒果 |
批发价 | 20 | 40 |
零售价 | 26 | 50 |
![]() 他购进的猕猴桃和芒果各多少千克?
他购进的猕猴桃和芒果各多少千克?
![]() 如果猕猴桃和芒果全部卖完,他能赚多少钱?
如果猕猴桃和芒果全部卖完,他能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
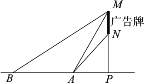
【题目】我校数学社团成员想利用所学的知识测量某广告牌的宽度(图中线段MN的长).直线MN垂直于地面,垂足为点P,在地面A处测得点M的仰角为60°,点N的仰角为45°,在B处测得点M的仰角为30°,AB=5米.且A、B、P三点在一直线上,请根据以上数据求广告牌的宽MN的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车油箱中有汽油![]() .如果不再加油,那么油箱中的油量
.如果不再加油,那么油箱中的油量![]() (单位:
(单位:![]() )随行驶路程
)随行驶路程![]() (单位:
(单位:![]() )的增加而减少.已知该汽车平均耗油量为
)的增加而减少.已知该汽车平均耗油量为![]() .
.
(Ⅰ)计算并填写下表:
| 10 | 100 | 300 | … |
| … |
(Ⅱ)写出表示![]() 与
与![]() 的函数关系式,并指出自变量
的函数关系式,并指出自变量![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,
,![]() 两地的路程约有
两地的路程约有![]() ,当油箱中油量少于
,当油箱中油量少于![]() 时,汽车会自动报警,则这辆汽车在由
时,汽车会自动报警,则这辆汽车在由![]() 地到
地到![]() 地,再由
地,再由![]() 地返回
地返回![]() 地的往返途中,汽车是否会报警?请说明理由.
地的往返途中,汽车是否会报警?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
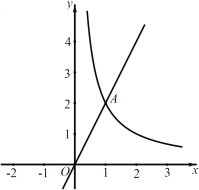
【题目】如图,直线![]() 与函数
与函数![]()
![]() 的图象交于点
的图象交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与函数
,与函数![]()
![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
①若点![]() 是线段
是线段![]() 的中点时,则点
的中点时,则点![]() 的坐标是______,
的坐标是______,![]() 的值是______;(直接写答案)
的值是______;(直接写答案)
②当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
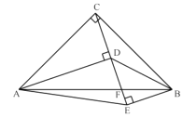
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 、
、![]() 向过点
向过点![]() 的直线作垂线,垂足分别为
的直线作垂线,垂足分别为![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)如图,求证:![]() ;
;
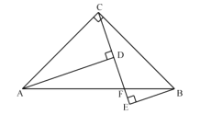
(2)如图,连接![]() 、
、![]() ,若
,若![]() ,在不添加任何辅助线的情况下,请直接写出四个角,使写出的每一个角的正切值都等于
,在不添加任何辅助线的情况下,请直接写出四个角,使写出的每一个角的正切值都等于![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com