
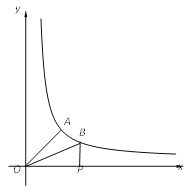
【题目】如图,已知A、B是反比例函数y=![]() 图象上两点,BP⊥x轴,垂足为P.已知∠AOP=45°,OA=4, tan∠BOP=
图象上两点,BP⊥x轴,垂足为P.已知∠AOP=45°,OA=4, tan∠BOP=![]() .
.
(1)求点A的坐标;
(2)连接AB,求四边形AOPB的面积.
【答案】(1)A(2![]() ,2
,2![]() );(2)4+2
);(2)4+2![]()
【解析】试题分析:(1)、过点A作AC⊥OP交OP于点C,根据等腰直角三角形的性质得出AC和OC的长度,从而得到点A的坐标;(2)、根据点A的坐标求出反比例函数解析式,根据∠BOP的正切值设点B的坐标为(2m,m),然后代入函数解析式求出m的值,最后根据四边形AOPB的面积等于四边形ACPB的面积加上△AOC的面积得出答案.
试题解析:(1)、过点A作AC⊥OP交 OP于点C 在Rt△AOC中,∵∠AOP=45°.
∴AC=OC=2![]() ,即A(2
,即A(2![]() ,2
,2![]() )
)
(2)把A(2![]() ,2
,2![]() )代入y=
)代入y= ![]() 得k=8,即y=
得k=8,即y= ![]()
在Rt△OBP中,tan∠BOP=![]() ,即OP=2BP,设BP=m,即B(2m,m)
,即OP=2BP,设BP=m,即B(2m,m)
把B(2m,m)代入y=![]() ,m=2,即BP=2,OP=4
,m=2,即BP=2,OP=4
∴S四边形AOPB=S四边形ACPB+S△CPB=![]() 2
2![]() 2
2![]() +
+![]() (2+2
(2+2![]() )(4-2
)(4-2![]() )=4+2
)=4+2![]()


科目:初中数学 来源: 题型:
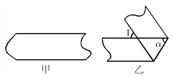
【题目】(1)有一条纸带如图甲所示,怎样检验纸带的两条边线是否平行?说明你的方法和理由.
(2)如图乙,将一条上下两边互相平行的纸带折叠,设∠1为x度,请用x的代数式表示∠α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
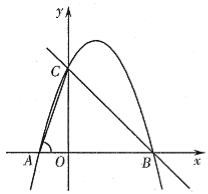
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+n与x轴、y轴分别交于B、C两点,抛物线y=ax2+bx+3(a≠0)过C、B两点,交x轴于另一点A,连接AC,且tan∠CAO=3.
(1)求抛物线的解析式;
(2)若点P是射线CB上一点,过点P作x轴的垂线,垂足为H,交抛物线于Q,设P点横坐标为t,线段PQ的长为d,求出d与t之间的函数关系式,并写出相应的自变量t的取值范围;
(3)在(2)的条件下,当点P在线段BC上时,设PH=e,已知d,e是以y为未知数的一元二次方程:y2-(m+3)y+![]() (5m2-2m+13)=0 (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.
(5m2-2m+13)=0 (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港珠澳大桥总长度5500000米被称为“新世界七大奇迹之一”,则数字5500000用科学记数法表示为( )
A.55×105B.55×106C.0.55×105D.5.5×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⑴ 一个数的平方等于它的本身的数是____________
⑵ 平方根等于它的本身的数是______________
⑶ 算术平方根等于它的本身的数是__________
⑷ 立方根等于它的本身的数是______________
⑸ 大于0且小于π的整数是________________
⑹ 满足![]() <x <
<x <![]() 的整数x是_______
的整数x是_______
查看答案和解析>>
科目:初中数学 来源: 题型:
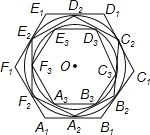
【题目】如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
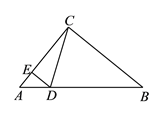
【题目】如图,在△ABC中(BC>AC),∠ACB=90°,点D在AB边上,DE⊥AC于点E.设点F在线段EC上,点G在射线CB上,以F,C,G为顶点的三角形与△EDC有一个锐角相等,FG交CD于点P,问:线段CP可能是△CFG的高线还是中线?或两者都有可能?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com