
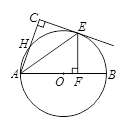
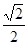 ,求OF的长.
,求OF的长. ……………………………… 1分
……………………………… 1分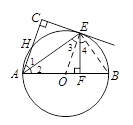 ∵ 点E为 的中点,
∵ 点E为 的中点,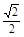 ,
,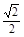 .
.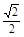 ,
, ∴ EF=
∴ EF= . ……………………………………………………………… 4分
. ……………………………………………………………… 4分 FO=90°,
FO=90°,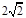 )2.
)2.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源:不详 题型:解答题

 =0.1736 ,
=0.1736 ,  =0.9848,
=0.9848, 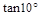 =0.1763.
=0.1763.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
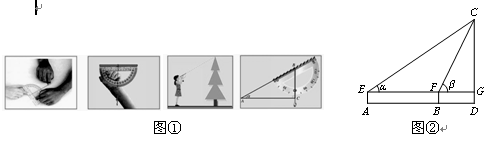
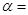 30°,再向楼的方向直行10米到达B处,又测得楼顶C的仰角
30°,再向楼的方向直行10米到达B处,又测得楼顶C的仰角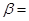 60°,若小红的目高(眼睛到地面的高度)AE为1.60米,请你帮助她计算出这座教学楼CD的高度(结果精确到0.1米,参考数据:
60°,若小红的目高(眼睛到地面的高度)AE为1.60米,请你帮助她计算出这座教学楼CD的高度(结果精确到0.1米,参考数据: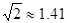 ,
,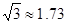 ,
, ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com