
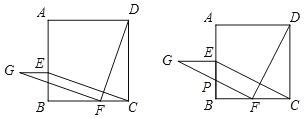
【题目】如图1,在正方形ABCD中,点E,F分别是边AB,BC上的点,且BE=CF.连结CE,DF.将线段FD绕点F逆时针旋转90°,得到线段FG.
(1)依题意将图1补全;
(2)连结EG,请判断:EG与CF的数量关系是 ,位置关系是 ;并证明你的结论;
(3)当FG经过BE中点时,写出求∠CDF度数的思路.

【答案】(1)见解析(2)EG与CF的数量关系是:EG=CF,位置关系是:EG∥CF;(3)当FG经过BE中点P时
【解析】分析:(1)根据要求画出图形即可;
(2)只要证明四边形EGFC是平行四边形即可;
(3)首先证明![]() ,求出
,求出![]() 即可解决问题.
即可解决问题.
详解:(1)如图所示:
 ;
;
(2)EG与CF的数量关系是:EG=CF,位置关系是:EG∥CF;
证明:∵正方形ABCD,
∴BC=CD,![]()
∵BE=CF,
∴△BCE≌△CDF
∴DF=CE,∠BEC=∠CFD.
∵![]()
∴![]()
即CE⊥DF,
∵线段FD绕点F逆时针旋转![]() ,得到线段FG,
,得到线段FG,
∴CE∥FG,DF=FG.
∴CE=FG.
∴四边形GFCE是平行四边形。
∴EG=CF,EG∥CF;
故答案为EG=CF,EG∥CF.
(3)当FG经过BE中点P时,
由△BCE≌△CDF,可得∠CDF=∠BCE.
由![]() ,可得∠BCE=∠G.
,可得∠BCE=∠G.
即∠CDF═∠G,
由BE=CF=GE,可得![]()
利用锐角三角函数,可求∠G的度数,从而可求∠CDF的度数.


科目:初中数学 来源: 题型:
【题目】如图在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,且a、b满足|2a+4|+|b-6|=0
![]()
(1)求A,B两点之间的距离;
(2)若在数轴上存在一点C,且AC=2BC,求C点表示的数;
(3)若在原点O处放一个挡板,一个小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动:设运动的时间为(秒).
①分别表示甲、乙两小球到原点的距离(用t表示);
②求甲、乙两小球到原点的距离相等时经历的时间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发前往B城.在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是( )
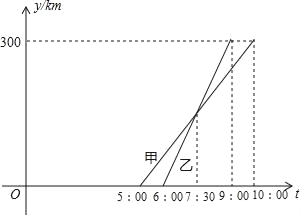
A. A城和B城相距300km
B. 甲先出发,乙先到达
C. 甲车的速度为60km/h,乙车的速度为100km/h
D. 6:00~7:30乙在甲前,7:30甲追上乙,7:30~9:00甲在乙前
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明星期天从家里出发骑车去舅舅家做客,当他骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是他本次去舅舅家所用的时间与路程的关系式示意图,根据图中提供的信息回答下列问题:
(1)小明家到舅舅家的路程是______米,小明在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小明骑车速度最快,最快的速度是多少米/
分?
(3)本次去舅舅家的行程中,小明一共行驶了多少米?一共用了多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知直线 AB、CD 相交于点 O,∠COE=90°
(1)若∠AOC=36°,求∠BOE 的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE 的度数.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923292236627968/1924724835590144/STEM/dc8ee683cff64dfdb92368e07f9f9b9d.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次科技作品制作比赛中,某小组8件作品的成绩(单位:分)分别是:7、10、9、8、7、9、9、8,对这组数据,下列说法正确的是( )
A. 众数是9B. 中位数是8C. 平均数是8D. 方差是7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com