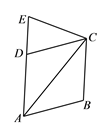
【题目】如图，点E是菱形ABCD的边AD延长线上的点，AE =AC，CE=CB，则∠B的度数为_______．
【答案】108 °
【解析】分析：设∠DAC的度数为x，利用菱形的性质得DA=DC，∠DCA=∠DAC=x，则利用三角形外角性质得∠EDC=2x，接着利用等腰三角形的性质得到∠E=∠EDC=2x，∠ACE=∠E=2x，于是利用三角形内角和定理得到x+2x+2x=180°，解得x=36°，然后计算出∠ADC的度数，从而得到∠B的度数．
详解：设∠DAC的度数为x．
∵四边形ABCD为菱形，∴DA=DC，∠ADC=∠B，∴∠DCA=∠DAC=x，∴∠EDC=∠DCA+∠DAC=2x．
∵CD=CE，∴∠E=∠EDC=2x．
∵AE=AC，∴∠ACE=∠E=2x，∴x+2x+2x=180°，解得：x=36°．
∵∠ADC=180°﹣2x=108°，∴∠B=∠ADC=108°．
故答案为：108°．
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案科目：初中数学 来源： 题型：
【题目】某地电话拨号上网有两种收费方式，用户可以任意选择其中一种：第一种是计时制，0.05元／分； 第二种是包月制，69元／月（限一部个人住宅电话上网）．此外，每一种上网方式都得加收通讯费0.02元／分．
（1）若小明家今年三月份上网的时间为
小时，请你分别写出两种收费方式下小明家应该支付的费用；
（2）若小明估计自家一个月内上网的时间为20小时，你认为采用哪种方式较为合算？
查看答案和解析>>
科目：初中数学 来源： 题型：
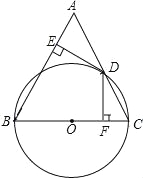
【题目】如图，在△ABC中，AB=BC，以BC为直径的⊙O交AC于点D，过点D作DE⊥AB，DF⊥BC，垂足分别为E、F．
（1）求证：ED是⊙O的切线；
（2）若DF=3
，cosA=
，求⊙O的直径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面的图形是由边长为l的正方形按照某种规律排列而组成的．
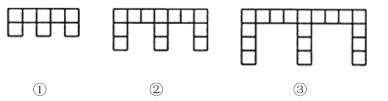
（1）观察图形，填写下表：
（2）推测第n个图形中，正方形的个数为 ，周长为 （都用含n的代数式表示）．
（3）这些图形中，任意一个图形的周长y与它所含正方形个数x之间的关系可表示为
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．
（1）求证：OE=OF；
（2）若CE=12，CF=5，求OC的长；
（3）当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点A（﹣2，0），点B（6，0），点C在第一象限内，且△OBC为等边三角形，直线BC交y轴于点D，过点A作直线AE⊥BD于点E，交OC于点E
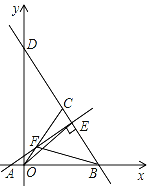
（1）求直线BD的解析式；（2）求线段OF的长；（3）求证：BF＝OE．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在四边形ABCD中,∠D=90°，AB=13，BC=12，CD=4，AD=3.
求：(1)AC的长度；
(2)判断△ACB是什么三角形?并说明理由?
(3)四边形ABCD的面积。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某体校要从四名射击选手中选拔一名参加省体育运动会，选拔赛中每名选手连续射靶10次，他们各自的平均成绩
及其方差S2如表所示：
甲 | 乙 | 丙 | 丁 | |
（环） | 8.4 | 8.6 | 8.6 | 7.6 |
S2 | 0.74 | 0.56 | 0.94 | 1.92 |
如果要选出一名成绩高且发挥稳定的选手参赛，则应选择的选手是（ ）
A．甲 B．乙 C．丙 D．丁
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在正方形ABCD中，点E，F分别是边AB，BC上的点，且BE=CF．连结CE，DF．将线段FD绕点F逆时针旋转90°，得到线段FG．
（1）依题意将图1补全；
（2）连结EG，请判断：EG与CF的数量关系是 ，位置关系是 ；并证明你的结论；
（3）当FG经过BE中点时，写出求∠CDF度数的思路．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com