
【题目】如图,已知点A(﹣2,0),点B(6,0),点C在第一象限内,且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD于点E,交OC于点E
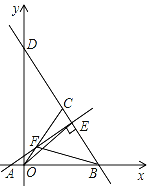
(1)求直线BD的解析式;(2)求线段OF的长;(3)求证:BF=OE.
【答案】(1)![]() ;(2)OF= 2;(3)见解析.
;(2)OF= 2;(3)见解析.
【解析】
(1)在Rt△ABD中,通过解直角三角形可求出OD的长,进而可得出点D的坐标,再根据点B,D的坐标,利用待定系数法可求出直线BD的解析式;
(2)由等边三角形的性质结合三角形内角和定理,可得出∠BAE=∠CFE=30°,进而可得出∠OAF=∠OFA=30°,再利用等角对等边可得出线段OF的长;
(3)通过解含30度角的直角三角形可求出BE的长,结合BC的长可得出CE=OF=2,由OB=CO,∠BOF=∠OCE及OF=CE可证出△OBF≌△COE(SAS),再利用全等三角形的性质可得出BF=OE.
(1)∵△OBC为等边三角形,
∴∠ABC=60°.
在Rt△ABD中,tan∠ABD=![]() ,即
,即![]() ,
,
∴AD=![]() ,
,
∴点D的坐标是(0,![]() ).
).
设BD的解析式是y=kx+b(k≠0),
将B(6,0),D(0,![]() )代入y=kx+b,得:
)代入y=kx+b,得: ,
,
解得: ,
,
∴直线BD的解析式为![]() .
.
(2)解:∵AE⊥BC,△OBC是正三角形,
∴∠BAE=∠CFE=30°,
∴∠OAF=∠OFA=30°,
∴OF=OA=2,即OF的长为2.
(3)证明:∵AB=8,∠OBC=60°,AE⊥BC,
∴BE=![]() AB=4,
AB=4,
∴CE=BC-BE=6-4=2,
∴OF=CE.
在△OBF和△COE中, ,
,
∴△OBF≌△COE(SAS),
∴BF=OE.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】共享单车被誉为“新四大发明”之一,如图1所示是某公司2017年向信阳市场提供一种共享自行车的实物图,车架档AC与CD的长分别为45cm,60cm,AC⊥CD,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离.(结果精确到1cm,参考数据:sin75°=0.9659,cos75°=0.2588,tan75°=3.7321)

查看答案和解析>>
科目:初中数学 来源: 题型:
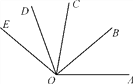
【题目】如图,OB为∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD为多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG.
(1)试说明四边形EFCG是矩形;
(2)当圆O与射线BD相切时,点E停止移动,在点E移动的过程中,
①矩形EFCG的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;
②求点G移动路线的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
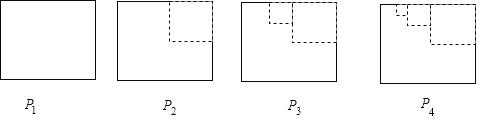
【题目】如图,P1是一块边长为1的正方形纸板,在P1的右上端剪去一个边长为![]() 的正方形后得到图形P2,然后依次剪去一个更小的正方形(其边长为前一个被剪去的正方形边长的一半)得到图形P3、P4、P5…,记纸板Pn的面积为Sn,则Sn﹣Sn+1的值为( )
的正方形后得到图形P2,然后依次剪去一个更小的正方形(其边长为前一个被剪去的正方形边长的一半)得到图形P3、P4、P5…,记纸板Pn的面积为Sn,则Sn﹣Sn+1的值为( )
A.(![]() )nB.(
)nB.(![]() )nC.(
)nC.(![]() )n+1D.(
)n+1D.(![]() )2n﹣1
)2n﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
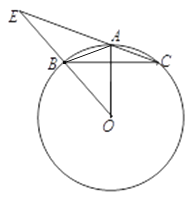
【题目】如图,△ABC内接于⊙O,AB=AC,连接并延长OB交CA延长线于点E.
(1)求证: OA平分∠BAC;
(2)若tan∠ABC=![]() ,AC=
,AC=![]() . 求⊙O的半径和线段BE的长.
. 求⊙O的半径和线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
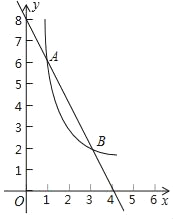
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
(m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
(1)求这两个函数的表达式;
(2)根据图象直接写出kx+b﹣![]() <0的x的取值范围.
<0的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知直线 AB、CD 相交于点 O,∠COE=90°
(1)若∠AOC=36°,求∠BOE 的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE 的度数.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923292236627968/1924724835590144/STEM/dc8ee683cff64dfdb92368e07f9f9b9d.png]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com