
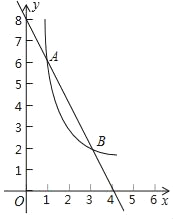
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
(m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
(1)求这两个函数的表达式;
(2)根据图象直接写出kx+b﹣![]() <0的x的取值范围.
<0的x的取值范围.
科目:初中数学 来源: 题型:
【题目】如图所示,一条自西向东的观光大道l上有A、B两个景点,A、B相距2km,在A处测得另一景点C位于点A的北偏东60°方向,在B处测得景点C位于景点B的北偏东45°方向,求景点C到观光大道l的距离.(结果精确到0.1km)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(﹣2,0),点B(6,0),点C在第一象限内,且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD于点E,交OC于点E
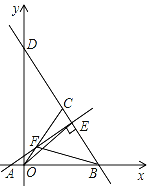
(1)求直线BD的解析式;(2)求线段OF的长;(3)求证:BF=OE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数形结合是数学解题中的一种重要思想,利用数轴可以将数与形完美结合.一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|,如:数轴上表示4和1的两点之间的距离是|4﹣1|=3;表示﹣3和2两点之间的距离是|﹣3﹣2|=5.
![]()
根据以上材料,结合数轴与绝对值的知识回答下列问题:
(1)将数﹣5,﹣![]() ,0,2.5在数轴上表示出来.
,0,2.5在数轴上表示出来.
(2)若数轴上表示数a的点位于﹣3与2之间,那么|a+3|+|a﹣2|的值是多少?
(3)若A是数轴上的一个点,它表示数a,则|a+5|+|a﹣3|的最小值是多少?当a取多少时|a+5|+|a﹣1|+|a﹣3|有最小值?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体校要从四名射击选手中选拔一名参加省体育运动会,选拔赛中每名选手连续射靶10次,他们各自的平均成绩![]() 及其方差S2如表所示:
及其方差S2如表所示:
甲 | 乙 | 丙 | 丁 | |
(环) | 8.4 | 8.6 | 8.6 | 7.6 |
S2 | 0.74 | 0.56 | 0.94 | 1.92 |
如果要选出一名成绩高且发挥稳定的选手参赛,则应选择的选手是( )
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户去年承包荒山若干亩,投资7800 元改造后,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售a元,在果园每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售1000千克,需8 人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
(1)分别用a,b表示两种方式出售水果的收入?
(2)若a=1.3元,b=1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
(3)该农户加强果园管理,力争到明年纯收入达到15000元,那么纯收入增长率是多少?(纯收入=总收入﹣总支出,该农户采用了(2)中较好的出售方式出售)
查看答案和解析>>
科目:初中数学 来源: 题型:
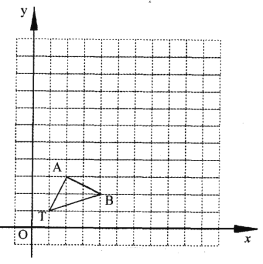
【题目】如图,在正方形网格中,△TAB 的顶点坐标分别为 T(1,1)、A(2,3)、B(4,2).
(1)以点 T(1,1)为位似中心,在位似中心的 同侧将△TAB 放大为原来的 3 倍,放大 后点 A、B 的对应点分别为 A'、B',画出△TA'B':
(2)写出点 A'、B'的坐标:A'( )、B'( );
(3)在(1)中,若 C(a,b)为线段 AB 上任一 点,则变化后点 C 的对应点 C'的坐标为 ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() ,
,![]() 重合),以
重合),以![]() 为边在
为边在![]() 右侧作正方形
右侧作正方形![]() ,连接
,连接![]() .
.
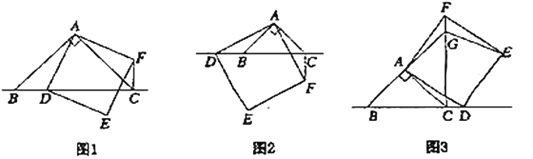
(1)观察猜想:如图1,当点![]() 在线段
在线段![]() 上时,
上时,
①![]() 与
与![]() 的位置关系为:______.②
的位置关系为:______.②![]() ,
,![]() ,
,![]() 之间的数量关系为:______;(将结论直接写在横线上)
之间的数量关系为:______;(将结论直接写在横线上)
(2)数学思考:如图2,当点![]() 在线段
在线段![]() 的延长线上时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
的延长线上时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸:如图3,当点![]() 在线段
在线段![]() 的延长线上时,延长
的延长线上时,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .若已知
.若已知![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在圆O的直径AB上,分别与BC和AC为直径在画两圆,然后用剪子或其它工具挖去这两个圆(即以O1、O2为圆心的圆),设BC=2R,AC=2r.
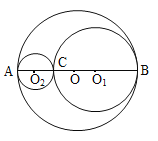
(1)求余下部分的面积(用R、r的代数式表示)
(2)当R≠r时,请你比较余下部分的面积和被挖去部分的面积的大小.
(3)当R=r时,请你比较余下部分的面积和被挖去部分的面积的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com