
【题目】如图,在圆O的直径AB上,分别与BC和AC为直径在画两圆,然后用剪子或其它工具挖去这两个圆(即以O1、O2为圆心的圆),设BC=2R,AC=2r.
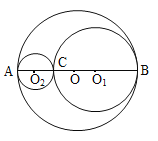
(1)求余下部分的面积(用R、r的代数式表示)
(2)当R≠r时,请你比较余下部分的面积和被挖去部分的面积的大小.
(3)当R=r时,请你比较余下部分的面积和被挖去部分的面积的大小.
【答案】(1)2Rrπ;(2)剩余的面积小于挖去的两圆面积和,(3)剩余的面积等于挖去的两圆面积和
【解析】
(1)用大圆的面积减去中间两个小圆的面积即可;
(2)当R≠r时,用被挖去部分的面积减去余下部分的面积,再判断值与0的关系即可;
(3)当R=r时,用被挖去部分的面积减去余下部分的面积,再判断值与0的关系即可;
解:(1)π(R+r)2-πr2-πR2=2Rrπ;
(2)R≠r时,(R2+r2)π-2Rrπ=(R2+r2-2Rr)π=(R-r)2π﹥0,
故(R2+r2)π﹥2Rrπ,
即剩余的面积小于挖去的两圆面积和,
(3)R=r时,(R2+r2)π-2Rrπ=(R2+r2-2Rr)π=(R-r)2π=0,
故(R2+r2)π=2Rrπ,
即剩余的面积等于挖去的两圆面积和


科目:初中数学 来源: 题型:
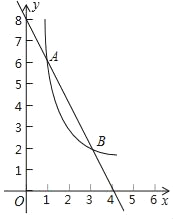
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
(m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
(1)求这两个函数的表达式;
(2)根据图象直接写出kx+b﹣![]() <0的x的取值范围.
<0的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知直线 AB、CD 相交于点 O,∠COE=90°
(1)若∠AOC=36°,求∠BOE 的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE 的度数.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923292236627968/1924724835590144/STEM/dc8ee683cff64dfdb92368e07f9f9b9d.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
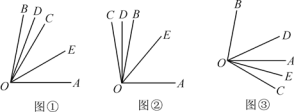
【题目】如图①,已知∠AOB=80°,OC是∠AOB内的一条射线,OD,OE分别平分∠BOC和∠COA.
(1)求∠DOE的度数;
(2)当射线OC绕点O旋转到OB的左侧时如图②(或旋转到OA的右侧时如图③),OD,OE仍是∠BOC和∠COA的平分线,此时∠DOE的大小是否和(1)中的答案相同?若相同,请选取一种情况写出你的求解过程;若不相同,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
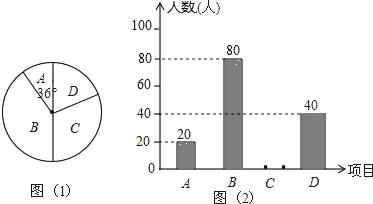
【题目】某学校为了提高学生学科能力,决定开设以下校本课程:A.文学院,B.小小数学家,C.小小外交家,D.未来科学家,为了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的小小外交家的课堂学习中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加全国英语口语大赛,求恰好同时选中甲、乙两位同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月初某水果批发商用4.3万元购得A种水果300箱,B种水果200箱,预计5月可全部销售完这些水果.
(1)若两种水果每箱的售价一样,该批发商想通过本次销售至少盈利10000元,则每箱水果菜至少卖多少元?(总利润=总销售额–总成本)
(2)6月份的时候,受天气的影响,两种水果的销售量比预计均下降了a%,其中B种水果保持(1)中最低售价不变,而A种水果比(1)中的最低售价下降了![]() %,结果导致两种水果的销售总额相等,求a的值.
%,结果导致两种水果的销售总额相等,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
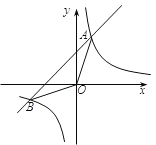
【题目】如图,反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于两点A(1,3),B(n,-1).
的图像交于两点A(1,3),B(n,-1).
⑴ k= ,n= ;
⑵ 求一次函数的表达式;
⑶ 结合图像直接回答:不等式![]() <mx+b解集是 ;
<mx+b解集是 ;
⑷ 求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com