
【题目】如图①,已知∠AOB=80°,OC是∠AOB内的一条射线,OD,OE分别平分∠BOC和∠COA.
(1)求∠DOE的度数;
(2)当射线OC绕点O旋转到OB的左侧时如图②(或旋转到OA的右侧时如图③),OD,OE仍是∠BOC和∠COA的平分线,此时∠DOE的大小是否和(1)中的答案相同?若相同,请选取一种情况写出你的求解过程;若不相同,请说明理由.
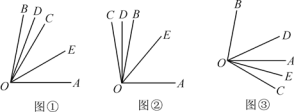
【答案】(1) 40°;(2) 40°.
【解析】
(1)利用角平分线定义,得出∠DOE=![]() ∠BOC+
∠BOC+![]() ∠AOC,然后根据∠AOB=80°即可求出∠DOE的度数;
∠AOC,然后根据∠AOB=80°即可求出∠DOE的度数;
(2)∠DOE的大小与(1)中答案相同,仍为40°.由角平分线的定义及角的和差即可得出结论.
(1)∵OD、OE分别是∠BOC和∠COA的平分线,∴∠COD=![]() ∠BOC,∠COE=
∠BOC,∠COE=![]() ∠AOC,∴∠DOE=∠COD+∠COE=
∠AOC,∴∠DOE=∠COD+∠COE=![]() ∠BOC+
∠BOC+![]() ∠AOC=
∠AOC=![]() ∠AOB=40°;
∠AOB=40°;
(2)∠DOE的大小与(1)中答案相同,仍为40°.选图②说明:∠DOE=∠COE-∠COD=![]() ∠AOC-
∠AOC-![]() ∠BOC=
∠BOC=![]() (∠AOC-∠BOC)=
(∠AOC-∠BOC)=![]() ∠AOB=
∠AOB=![]() ×80°=40°.
×80°=40°.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】已知AB∥CD.
如图1,你能得出∠A+∠E+∠C=360°吗?
如图2,猜想出∠A.∠C、∠E的关系式并说明理由.
如图3,∠A.∠C、∠E的关系式又是什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.“寒假”期间,某校小记者随机调查了某地区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图1;
(2)求图2中表示家长“赞成”的圆心角的度数;
(3)已知某地区共6500名家长,估计其中反对中学生带手机的大约有多少名家长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.


图1 图2
(1)如图1,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的平分线,求∠BON和∠CON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年4月20日,四川雅安发生7.0级地震,给雅安人民的生命财产带来巨大损失.某市民政部门将租用甲、乙两种货车共16辆,把粮食266吨、副食品169吨全部运到灾区.已知一辆甲种货车同时可装粮食18吨、副食品10吨;一辆乙种货车同时可装粮食16吨、副食11吨.
(1)若将这批货物一次性运到灾区,有哪几种租车方案?
(2)若甲种货车每辆需付燃油费1500元;乙种货车每辆需付燃油费1200元,应选(1)中的哪种方案,才能使所付的费用最少?最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一列有理数﹣1,2,﹣3,4,﹣5,6,……,按如图所示有序排列,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰6”中D的位置是有理数( ),2008应排在A、B、C、D、E中的( ) 位置.其中两个填空依次为( )

A. 29,C B. ﹣29,D C. 30,B D. ﹣31,E
查看答案和解析>>
科目:初中数学 来源: 题型:
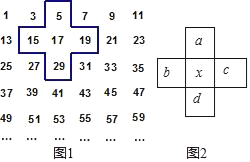
【题目】如图,将连续的奇数1,3,5,7…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.
(1)若x=17,则a+b+c+d= .
(2)移动十字框,用x表示a+b+c+d= .
(3)设M=a+b+c+d+x,判断M的值能否等于2020,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2![]() ,P是AC上的一个动点.
,P是AC上的一个动点.

(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时□DPBQ的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com