
【题目】![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() ,
,![]() 重合),以
重合),以![]() 为边在
为边在![]() 右侧作正方形
右侧作正方形![]() ,连接
,连接![]() .
.
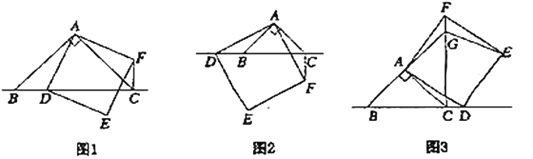
(1)观察猜想:如图1,当点![]() 在线段
在线段![]() 上时,
上时,
①![]() 与
与![]() 的位置关系为:______.②
的位置关系为:______.②![]() ,
,![]() ,
,![]() 之间的数量关系为:______;(将结论直接写在横线上)
之间的数量关系为:______;(将结论直接写在横线上)
(2)数学思考:如图2,当点![]() 在线段
在线段![]() 的延长线上时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
的延长线上时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸:如图3,当点![]() 在线段
在线段![]() 的延长线上时,延长
的延长线上时,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .若已知
.若已知![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长.
的长.
【答案】观察猜想:(1)①![]() ; ②
; ②![]() ;数学思考:(2)结论①
;数学思考:(2)结论①![]() 仍然成立,见解析,结论②变为
仍然成立,见解析,结论②变为![]() ,见解析;拓展延伸:(3)
,见解析;拓展延伸:(3)![]() .
.
【解析】
(1)根据正方形的性质证明△DAB≌△FAC,根据全等三角形的性质即可得到结论;
(2)根据正方形的性质证明△DAB≌△FAC,再根据等腰直角三角形的性质即可求解;
(3)分别过点![]() 、
、![]() 作垂线,根据(1)(2)的结论,再证明
作垂线,根据(1)(2)的结论,再证明![]() ,根据勾股定理即可求解.
,根据勾股定理即可求解.
解:(1)在正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,故△DAB≌△FAC
∴∠B=∠ACF,∴∠ACB+∠ACF=90°,即
![]()
②∵△DAB≌△FAC
∴CF=BD,
∵BC=BD+CD,
∴BC=CF+CD
(2)结论①![]() 仍然成立,结论②变为
仍然成立,结论②变为![]() .
.
证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() .
.
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() .
.
设![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() 即
即![]()
(3)分别过点![]() 、
、![]() 作垂线,类比(1)(2)结论可知
作垂线,类比(1)(2)结论可知![]() ,
,![]() ,
,![]() ,
,
又AD=DE,∠AND=∠DHE=90°,
∵∠NAD+∠ADN=90°,∠EDH+∠ADN=90°,
∴∠NAD=∠EDH
∴![]()
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得![]()


科目:初中数学 来源: 题型:
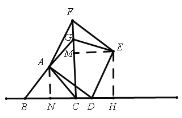
【题目】如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG.
(1)试说明四边形EFCG是矩形;
(2)当圆O与射线BD相切时,点E停止移动,在点E移动的过程中,
①矩形EFCG的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;
②求点G移动路线的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
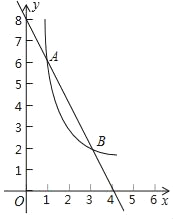
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
(m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
(1)求这两个函数的表达式;
(2)根据图象直接写出kx+b﹣![]() <0的x的取值范围.
<0的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料
“一带一路”建设将以政策沟通、设施联通、贸易畅通、资金融通、民心相通为主要内容,为沿线国家发展和世界经济注入新动力.中国与“一带一路”沿线国家合作具有较好的基础.2012年中国与沿线国家的货物贸易额占中国货物贸易总额的24.8%,2013年中国与沿线国家的货物贸易额占中国货物贸易总额的25.0%.随着“一带一路”战略的实施,中国与“一带一路”沿线国家的贸易规模不断扩大,2014年,中国与沿线国家的货物贸易额达到1.12万亿美元,占中国货物贸易总额的26.1%.2015年,中国与沿线国家的货物贸易额达到0.93万亿美元,占中国货物贸易总额的25.3%.2016年,中国与沿线国家贸易额为0.95万亿美元,占中国货物贸易总额的25.7%.“一带一路”建设为我们打开了新思路,世界期待,为促进世界经济增长、深化地区合作打造更坚实的发展基础,更好地造福了各国人民.
根据以上材料解答下列问题:
(1)请你用统计图将2012﹣2016年中国与“一带一路”沿线国家的货物贸易额占中国货物贸易总额的百分比表示出来,并在图中标明相应数据;
(2)根据材料预估2017年中国与“一带一路”沿线国家贸易额约为 万亿美元,你估计的理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发前往B城.在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是( )
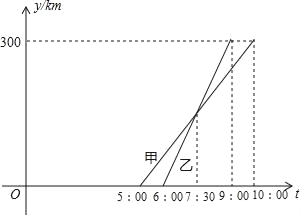
A. A城和B城相距300km
B. 甲先出发,乙先到达
C. 甲车的速度为60km/h,乙车的速度为100km/h
D. 6:00~7:30乙在甲前,7:30甲追上乙,7:30~9:00甲在乙前
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山若干亩,今年水果总产量为18000 千克,此水果在市场上每千克售 a 元,在果园每千克售b 元( b a ),该农户将水果拉到市场出售平均每天出售1000 千克,需8 人帮忙,每人每天付工资 25 元,农用车运费及其他各项税费平均每天100 元.
(1)分别用 a,b 表示两种方式出售水果的收入;
(2)若 a1.3元, b1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知直线 AB、CD 相交于点 O,∠COE=90°
(1)若∠AOC=36°,求∠BOE 的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE 的度数.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923292236627968/1924724835590144/STEM/dc8ee683cff64dfdb92368e07f9f9b9d.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
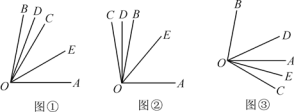
【题目】如图①,已知∠AOB=80°,OC是∠AOB内的一条射线,OD,OE分别平分∠BOC和∠COA.
(1)求∠DOE的度数;
(2)当射线OC绕点O旋转到OB的左侧时如图②(或旋转到OA的右侧时如图③),OD,OE仍是∠BOC和∠COA的平分线,此时∠DOE的大小是否和(1)中的答案相同?若相同,请选取一种情况写出你的求解过程;若不相同,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
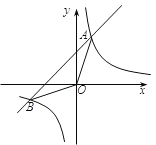
【题目】如图,反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于两点A(1,3),B(n,-1).
的图像交于两点A(1,3),B(n,-1).
⑴ k= ,n= ;
⑵ 求一次函数的表达式;
⑶ 结合图像直接回答:不等式![]() <mx+b解集是 ;
<mx+b解集是 ;
⑷ 求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com