练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】共享单车被誉为“新四大发明”之一，如图1所示是某公司2017年向信阳市场提供一种共享自行车的实物图，车架档AC与CD的长分别为45cm，60cm，AC⊥CD，座杆CE的长为20cm，点A，C，E在同一条直线上，且∠CAB=75°，如图2．

    （1）求车架档AD的长；

    （2）求车座点E到车架档AB的距离．（结果精确到1cm，参考数据：sin75°=0.9659，cos75°=0.2588，tan75°=3.7321）

    【答案】（1）75cm (2) 63cm

    【解析】分析：（1）根据AC、CD和AC⊥CD可以求得AD的长；

    （2）根据AC、CE和∠EAF的度数可以求得EF的长．

    详解：（1）∵AC⊥CD，AC=45cm，CD=60cm，

    ∴AD=（cm），

    即车架档AD的长是75cm；

    （2）作EF⊥AB于点F，如图所示，

    ∵AC=45cm，EC=20cm，∠EAB=75°，

    ∴EF=AEsin75°=（45+20）×0.9659≈63cm，

    即车座点E到车架档AB的距离是63cm．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

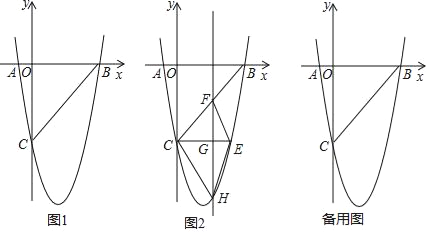
    【题目】如图1，在平面直角坐标系中，已知抛物线y=ax2+bx﹣5与x轴交于A（﹣1，0），B（5，0）两点，与y轴交于点C．

    （1）求抛物线的函数表达式；

    （2）如图2，CE∥x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC，CE分别相交于点F，G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标；

    （3）若点K为抛物线的顶点，点M（4，m）是该抛物线上的一点，在x轴，y轴上分别找点P，Q，使四边形PQKM的周长最小，求出点P，Q的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，点A在原点左侧，点B在原点右侧，且点A到原点的距离是点B到原点距离的2倍，AB=15.

    （1）点A表示的数为________，点B表示的数为________；

    （2）点P从点A出发，以每秒1个单位长度的速度向点B方向运动；同时，点Q从点B出发，先向点A方向运动，当与点P重合后，马上改变方向与点P同向而行且速度始终为每秒2个单位长度。设运动时间为t秒。

    ①当点P与点Q重合时，求t的值；

    ②当点P是线段AQ的三等分点时，求t的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学习千万条，思考第一条。请你用本学期所学知识探究以下问题：

    （1）已知点为直线上一点，将直角三角板的直角顶点放在点处，并在内部作射线．

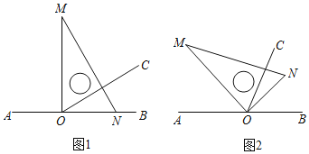
    ①如图1，三角板的一边与射线重合，且，若以点为观察中心，射线表示正北方向，求射线表示的方向；

    ②如图2，将三角板放置到如图位置，使恰好平分，且，求的度数.

    （2）已知点不在同一条直线上，，平分，平分，用含的式子表示的大小.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某地电话拨号上网有两种收费方式，用户可以任意选择其中一种：第一种是计时制，0.05元／分； 第二种是包月制，69元／月（限一部个人住宅电话上网）．此外，每一种上网方式都得加收通讯费0.02元／分．

    （1）若小明家今年三月份上网的时间为小时，请你分别写出两种收费方式下小明家应该支付的费用；

    （2）若小明估计自家一个月内上网的时间为20小时，你认为采用哪种方式较为合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在生活中，人们经常通过一些标志性建筑确定位置，在数学中往往也是这样．

    （1）将正整数如图1的方式进行排列：

    小明同学通过仔细观察，发现每一行第一列的数字有一定的规律，所以每一行第一列的数字可以作为标志数，于是他认为第七行第一列的数字是　 　，第7行、第5列的数字是　 　．

    （2）方法应用

    观察下面一列数：1，﹣2，3，﹣4，5，﹣6，7，…并将这列数按照如图2方式进行排列：

    按照上述方式排列下去，

    问题1：第10行从左边数第9个数是　 　；

    问题2：第n行有　 　个数；（用含n的代数式表示）

    问题3：数字2019在第　 　行，从左边数第　 　个数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

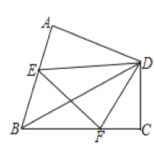
    【题目】如图，在四边形ABCD中，∠A=∠C=90°，∠B=α，在AB，BC上分别找一点E,F,使△DEF的周长最小，此时，∠EDF=______。（用含α的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，一条自西向东的观光大道l上有A、B两个景点，A、B相距2km，在A处测得另一景点C位于点A的北偏东60°方向，在B处测得景点C位于景点B的北偏东45°方向，求景点C到观光大道l的距离．（结果精确到0.1km）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知点A（﹣2，0），点B（6，0），点C在第一象限内，且△OBC为等边三角形，直线BC交y轴于点D，过点A作直线AE⊥BD于点E，交OC于点E

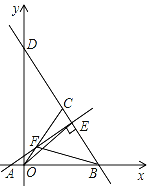
    （1）求直线BD的解析式；（2）求线段OF的长；（3）求证：BF＝OE．

    查看答案和解析>>

    同步练习册答案