
����Ŀ���������У����Ǿ���ͨ��һЩ��־�Խ���ȷ��λ�ã�����ѧ������Ҳ��������
��1������������ͼ1�ķ�ʽ�������У�

С��ͬѧͨ����ϸ�۲죬����ÿһ�е�һ�е�������һ���Ĺ��ɣ�����ÿһ�е�һ�е����ֿ�����Ϊ��־������������Ϊ�����е�һ�е��������� ������7�С���5�е��������� ����
��2������Ӧ��
�۲�����һ������1����2��3����4��5����6��7��������������������ͼ2��ʽ�������У�
����������ʽ������ȥ��
����1����10��������9�������� ����
����2����n������ �����������ú�n�Ĵ���ʽ��ʾ��
����3������2019�ڵ��� ���У������������ ��������
���𰸡���1��49��45����2����90��2n��1��45��83��
��������
��1���ҳ����ɵ�n�е�һ�е�����Ϊn2�����ɵó��������2���ҳ�����ÿһ����ĩ�����ֵľ���ֵ��������ƽ�֣�������ȡ����ֵ������������������������������Ϊ��������ż��Ϊ������������1����9����ĩ�����ֵľ���ֵ��81����10�д��������9�����ľ���ֵ��81+9��90����ż��Ϊ���������ʵ�10�д��������9�����ǩ�90������2����ÿ�����ĸ���Ϊ1��3��5��7�������n����2n��1����������3����2019��442+83�����ɵó������
�⣺��1����ÿһ�е�һ�е�����Ϊ���е�ƽ�֣�
����n�е�һ�е�����Ϊn2��
������е�һ�е������ǣ�72��49��
��5�е������ǣ�49��4��45��
�ʴ�Ϊ��49��45��
��2��������ã�ÿһ����ĩ�����ֵľ���ֵ��������ƽ�֣�������ȡ����ֵ������������������������������Ϊ��������ż��Ϊ��������ÿ�����ĸ���Ϊ��1��3��5��7����
����1���ߵ�9����ĩ�����ֵľ���ֵ��81��
���10�д��������9�����ľ���ֵ��81+9��90��
��ż��Ϊ��������
���10�д��������9�����ǩ�90��
����2����ÿ�����ĸ���Ϊ��1��3��5��7����
���n����2n��1������
����3����2019��442+83��
������2019�ڵ�45�У����������83������
�ʴ�Ϊ����90��2n��1��45��83��


 ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���۲�˼������ͼ���߶�AB����������C��D����ֱ�д���Ե�A��B��C��DΪ�˵���߶Σ�������ͼ�й��ж������߶Σ�
��2��ģ����������߶�����m���㣨�����߶ε������˵㣩������߶��Ϲ��ж������߶Σ���˵������۵���ȷ�ԣ�
��3����չӦ�ã�ij��45��ͬѧ�ڱ�ҵ���һ�ξۻ��У���ÿ������1�����ʺã���ô���ն��ٴ��֣�
�뽫�������ת��Ϊ����ģ�ͣ���ֱ��Ӧ������ģ�͵Ľ��۽�����⣮
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��y=��![]() x+1��y���ڵ�B����x���ڵ�A��������y=��
x+1��y���ڵ�B����x���ڵ�A��������y=��![]() x2+bx+c������B����ֱ��y=��
x2+bx+c������B����ֱ��y=��![]() x+1���ڵ�C��4����2����
x+1���ڵ�C��4����2����
��1���������ߵĽ���ʽ��
��2����ͼ��������Ϊm�ĵ�M��ֱ��BC�Ϸ����������ϣ�����M��ME��y�ύֱ��BC�ڵ�E����MEΪֱ����Բ��ֱ��BC����һ��D������E��x����ʱ������DEM���ܳ���
��3������AOB������ƽ���ڵ�ijһ�㰴˳ʱ�뷽����ת90�����õ���A1O1B1����A��O��B�Ķ�Ӧ��ֱ��ǵ�A1��O1��B1������A1O1B1����������ǡ�������������ϣ���ֱ��д����A1�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O����ABC��һ�㣬����OB��OC������AB��OB��OC��AC���е�D��E��F��G�������ᣬ�õ��ı���DEFG��
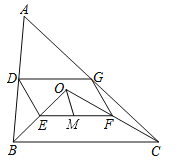
��1����֤���ı���DEFG��ƽ���ı��Σ�
��2����MΪEF���е㣬OM=3����OBC����OCB���࣬��DG�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������Ϊ�����Ĵ�����֮һ����ͼ1��ʾ��ij��˾2017���������г��ṩһ�ֹ������г���ʵ��ͼ�����ܵ�AC��CD�ij��ֱ�Ϊ45cm��60cm��AC��CD������CE�ij�Ϊ20cm����A��C��E��ͬһ��ֱ���ϣ��ҡ�CAB=75������ͼ2��
��1���ܵ�AD�ij���
��2��������E�����ܵ�AB�ľ��룮�������ȷ��1cm���ο����ݣ�sin75��=0.9659��cos75��=0.2588��tan75��=3.7321��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��A��B������Ʒ��100��������3100Ԫ������ۺ��ۼ����±���
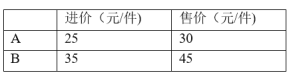
��1��A��B������Ʒ�ֱ����ټ�?
��2��������Ʒ�����ȡ�������Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
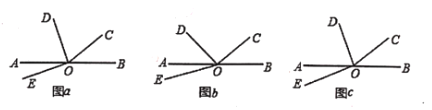
����Ŀ����ͼ��OΪֱ��AB��һ�㣬��BOC��36��.
��1)��ODƽ�֡�AOC����DOE��90������ͼ��a)��ʾ�����AOE�Ķ�����
��2)����AOD��![]() ��AOC����DOE��60������ͼ(b����ʾ�����AOE�Ķ�����
��AOC����DOE��60������ͼ(b����ʾ�����AOE�Ķ�����
��3������AOD��![]() ��AOC����DOE��
��AOC����DOE��![]() (n��2����nΪ������)����ͼ(c)��ʾ������n���Ĵ���ʽ��ʾ��AOE�Ķ���__________(ֱ��д�����).
(n��2����nΪ������)����ͼ(c)��ʾ������n���Ĵ���ʽ��ʾ��AOE�Ķ���__________(ֱ��д�����).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD��ֱ�����Σ�AB=18cm��CD=15cm��AD=6cm����P��B�㿪ʼ����BA�����A��1cm/s���ٶ��ƶ�����Q��D�㿪ʼ����DC�����C��2cm/s���ٶ��ƶ������P��Q�ֱ��B��Dͬʱ������P��Q��һ�㵽���յ�ʱ�˶�ֹͣ�����ƶ�ʱ��Ϊt��
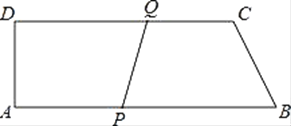
��1��tΪ��ֵʱ�ı���PQCB��ƽ���ı��Σ�
��2��tΪ��ֵʱ�ı���PQCB�Ǿ��Σ�
��3��tΪ��ֵʱ�ı���PQCB�ǵ������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
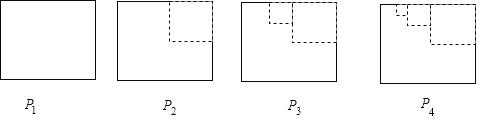
����Ŀ����ͼ��P1��һ��߳�Ϊ1��������ֽ�壬��P1�����϶˼�ȥһ���߳�Ϊ![]() �������κ�õ�ͼ��P2��Ȼ�����μ�ȥһ����С�������Σ���߳�Ϊǰһ������ȥ�������α߳���һ�룩�õ�ͼ��P3��P4��P5������ֽ��Pn�����ΪSn����Sn��Sn+1��ֵΪ��������
�������κ�õ�ͼ��P2��Ȼ�����μ�ȥһ����С�������Σ���߳�Ϊǰһ������ȥ�������α߳���һ�룩�õ�ͼ��P3��P4��P5������ֽ��Pn�����ΪSn����Sn��Sn+1��ֵΪ��������
A.��![]() ��nB.��
��nB.��![]() ��nC.��
��nC.��![]() ��n+1D.��
��n+1D.��![]() ��2n��1
��2n��1
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com