
【题目】如图,ABCD是直角梯形,AB=18cm,CD=15cm,AD=6cm,点P从B点开始,沿BA边向点A以1cm/s的速度移动,点Q从D点开始,沿DC边向点C以2cm/s的速度移动,如果P、Q分别从B、D同时出发,P、Q有一点到达终点时运动停止,设移动时间为t.
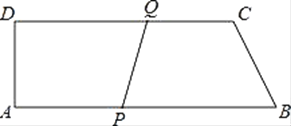
(1)t为何值时四边形PQCB是平行四边形?
(2)t为何值时四边形PQCB是矩形?
(3)t为何值时四边形PQCB是等腰梯形?
【答案】(1)当t=5时,四边形PQCB是平行四边形;(2)BC与AB不垂直,所以PQCB不可能是矩形;(3)当t=7时,四边形PQCB是菱形.
【解析】
(1)若四边形PQCB是平行四边形,则QC=PB,即DC-2t=t,求出t的值即可;
(2)由于BC与AB不垂直,所以无论t为何值,四边形PQCB都不可能是矩形;
(3)分别过点Q、C作QM⊥AB、CN⊥AB,由于梯形ABCD是直角梯形,故四边形AMQD是矩形,BN=AB-CD,
因为四边形PQCB是等腰梯形,故PM=BN,由此即可得出t的值.
解:
(1)∵四边形PQCB是平行四边形,
∴QC=PB,即DC-2t=t,
∴15-2t=t,解得t=5;
(2)∵BC与AB不垂直,
∴无论t为何值,四边形PQCB都不可能是矩形;
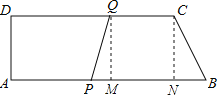
(3)分别过点Q、C作QM⊥AB、CN⊥AB,
∵梯形ABCD是直角梯形,AB=18cm,CD=15cm
∴四边形AMQD是矩形,BN=AB-CD=18-15=3cm,
∵四边形PQCB是等腰梯形,
∴PM=BN=3cm,
∴DQ=BP-PM,即2t=18-t+3,解得t=7(秒).


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
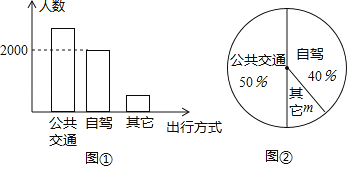
A. 本次抽样调查的样本容量是5000
B. 扇形图中的m为10%
C. 样本中选择公共交通出行的有2500人
D. 若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在生活中,人们经常通过一些标志性建筑确定位置,在数学中往往也是这样.
(1)将正整数如图1的方式进行排列:

小明同学通过仔细观察,发现每一行第一列的数字有一定的规律,所以每一行第一列的数字可以作为标志数,于是他认为第七行第一列的数字是 ,第7行、第5列的数字是 .
(2)方法应用
观察下面一列数:1,﹣2,3,﹣4,5,﹣6,7,…并将这列数按照如图2方式进行排列:
按照上述方式排列下去,
问题1:第10行从左边数第9个数是 ;
问题2:第n行有 个数;(用含n的代数式表示)
问题3:数字2019在第 行,从左边数第 个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
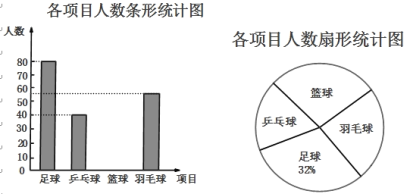
(1)这次活动一共调查了名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于多少度;
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一条自西向东的观光大道l上有A、B两个景点,A、B相距2km,在A处测得另一景点C位于点A的北偏东60°方向,在B处测得景点C位于景点B的北偏东45°方向,求景点C到观光大道l的距离.(结果精确到0.1km)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价不低于50元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件,设每件商品的售价为x元,每月的销售量为y件.
(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知直角三角形纸板ABC,直角边AB=4 cm,BC=8 cm.
(1)将直角三角形纸板ABC绕三角形的边所在的直线旋转一周,能得到_____种不同的几何体;
(2)分别计算绕三角形直角边所在的直线旋转一周,得到几何体的体积.(![]() 取3)
取3)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户去年承包荒山若干亩,投资7800 元改造后,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售a元,在果园每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售1000千克,需8 人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
(1)分别用a,b表示两种方式出售水果的收入?
(2)若a=1.3元,b=1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
(3)该农户加强果园管理,力争到明年纯收入达到15000元,那么纯收入增长率是多少?(纯收入=总收入﹣总支出,该农户采用了(2)中较好的出售方式出售)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com