练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
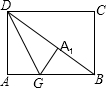
    如图，在矩形纸片ABCD中，AB=8，AD=6，折叠纸片使AD边与对角线BD重合，折痕为DG，点A落在点A1处，则AG的长为（　　）
    A、2B、3C、4D、5
    考点：翻折变换（折叠问题）
    专题：
    分析：根据勾股定理可得BD=10，由折叠的性质可得△ADG≌△A1DG，则A1D=AD=6，A1G=AG，则A1B=10-6=4，在Rt△A1BG中根据勾股定理求AG的即可．
    解答：解：在Rt△ABD中，AB=8，AD=6，
    则BD=
    		AB2+AD2
    =
    		82+62
    =10，
    由折叠的性质可得：△ADG≌△A1DG，
    ∴A1D=AD=6，A1G=AG，
    ∴A1B=10-6=4，
    设AG=x，则：A1G=AG=x，BG=8-x，
    在Rt△A1BG中，x2+42=（8-x）2
    解得：x=3，
    即AG长为3．
    故选B．
    点评：此题主要考查折叠的性质，综合利用了勾股定理的知识，认真分析图中各条线段的关系是解题的关键，难度一般．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

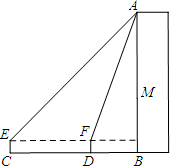    黄冈市高效课堂现场会在英山实验中学召开，为营造氛围，举办方从教学楼顶端A点处向下悬挂“优化教学方法，构建高效课堂”大型标语．九年级学生王港用高1m的测角仪在地面C点测得楼顶A点的仰角为45°，沿CB方向前进15m到达D点，测得A点仰角的正切值为
    8
    3
    ，若标语底端M点距地面9m，请你计算标语AM的长度为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

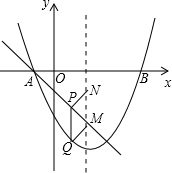    如图，抛物线y=ax2+bx-
    5
    2
    过点A（-1，0）、B（5，0）．直线y=-x-1交抛物线的对称轴于点M，点P为线段AM上一点，过点P作PQ∥y轴交抛物线于点Q，过点P作PN∥QM交抛物线的对称轴于点N，设点P的横坐标为m．
    （1）求a、b的值．
    （2）用含m的代数式表示PQ的长并求PQ的最大值．
    （3）直接写出PQ随m的增大而减小时m的取值范围．
    （4）当四边形PQMN是正方形时，求出m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    因式分解-2a2+8ab-8b2结果正确的是（　　）
    A、-2（a2-4ab+4b2）
    B、-2（a-2b）2
    C、-2（a+2b）2
    D、2（a-2b）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

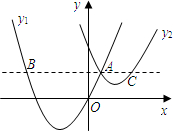    如图，抛物线y1=a（x+2）2+c与y2=
    1
    2
    （x-3）2+b交于点A（1，3），且抛物线y1经过原点．过点A作x轴的平行线，分别交两条抛物线于点B，C．则下列结论中，正确的是（　　）
    A、c=4a
    B、a=1
    C、当x=0时，y2-y1=4
    D、2AB=3AC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    先化简，后求值：[（2x-y）2-y（2x+y）]÷（-2x），其中x=-
    3
    2
    ，y=
    1
    3
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解方程：
    7
    x+x2
    -
    3
    x-x2
    =1-
    x2-7
    x2-1
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    定义：f（a，b）是关于 a、b的多项式，如果f（a，b）=f（b，a），那么f（a，b）叫做关于“对称多项式”．例如，如果f（a，b）=a2+a+b+b2，则f（b，a）=b2+b+a+a2，显然f（a，b）=f（b，a），所以f（a，b）是“对称多项式”．
    （1）f（a，b）=a2-2ab+b2是“对称多项式”，试说明理由；
    （2）请写一个“对称多项式”，f（a，b）=
     
    （不多于四项）；
    （3）如果f1（a，b）和f2（a，b）均为“对称多项式”，那么f1（a，b）+f2（a，b）一定是“对称多项式”吗？如果一定，说明理由，如果不一定，举例说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    a2•a4=
     

    （-2x2）•（-3xy）=
     
    ．

    查看答案和解析>>

    同步练习册答案