
如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.有下列结论:
①∠DEO=45°;
②△AOD≌△COE;
③S四边形CDOE = S△ABC;
S△ABC;
④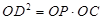 .
.
其中正确的结论序号为 .(把你认为正确的都写上)
①②③④.
解析试题分析:证△AOD≌△COE,推出OD=OE,即可判断①②;根据全等得出两三角洲的面积相等,即可推出△ACB的面积=四边形CDOE的面积的2倍,即可判断③;证△OEP∽△OCE,得出比例式,即可判断④.
试题解析::∵在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,
∴∠A=∠B=∠ACO=°,OA=OC=OB,∠AOC=90°=∠DOE,
∴∠AOD=∠COE=90°-∠DOC,
在△AOD与△COE中,
∴△AOD≌△COE(ASA),
∴OD=OE,
∵∠EOD=90°,
∴∠DEO=45°,
∵△AOD≌△COE,∴S△AOD=S△COE,
∴S四边形CDOE=S△COD+S△COE=S△COD+S△AOD=S△AOC= S△ABC,
S△ABC,
∵△DOE为等腰直角三角形,
∴∠DEO=45°.
∵∠DEO=∠OCE=45°,∠COE=∠COE,
∴△OEP∽△OCE,
∴ ,即OP•OC=OE2,
,即OP•OC=OE2,
即①②③④都正确;
考点:1.全等三角形的判定与性质;2.等腰直角三角形;3.相似三角形的判定与性质.


科目:初中数学 来源: 题型:解答题
已知:如图ΔABC中,D、E、F分别是AB、AC、BC的中点.
(1)若AB=10cm,AC=6cm,则四边形ADFE的周长为______cm
(2)若ΔABC周长为6cm,面积为12cm2,则ΔDEF的周长是 _____,面积是_____
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交边AD于点F,交CD的延长线于点G.
(1)求证:△APB≌△APD;
(2)已知DF∶FA=1∶2,设线段DP的长为x,线段PF的长为y.
①求y与x的函数关系式;
②当x=6时,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC, BE,AD相交于点G,过点B作BF∥AC交AD的延长线于点F, DF="6."
(1) 求AE的长;
(2) 求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在Rt△ABC中,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,
且DM⊥DN,作MF⊥AB于点F,NE⊥AB于点E。
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC。
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在□ABCD中,AB=4,AD=6,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG= .
.
(1)求AE的长; (2)求ΔCEF的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(1)如图1,在等边△ABC中,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等边△AMN,联结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是边BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.联结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com