
如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交边AD于点F,交CD的延长线于点G.
(1)求证:△APB≌△APD;
(2)已知DF∶FA=1∶2,设线段DP的长为x,线段PF的长为y.
①求y与x的函数关系式;
②当x=6时,求线段FG的长.
(1)证明见解析;(1)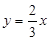 ;5.
;5.
解析试题分析:(1)根据菱形的性质得出∠DAP=∠PAB,AD=AB,再利用全等三角形的判定得出△APB≌△APD;
(2)①首先证明△DFP≌△BEP,进而得出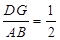 ,
,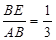 ,进而得出
,进而得出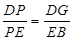 ,即
,即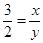 ,即可得出答案;
,即可得出答案;
②根据①中所求得出PF=PE=4,DP=PB=6,进而得出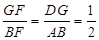 ,求出即可.
,求出即可.
试题解析:(1)证明:∵点P是菱形ABCD对角线AC上的一点,
∴∠DAP=∠PAB,AD=AB,
∵在△APB和△APD中 ,
,
∴△APB≌△APD(SAS);
(2)解:①∵△APB≌△APD,
∴DP=PB,∠ADP=∠ABP,
∵在△DFP和△BEP中,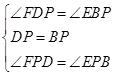 ,
,
∴△DFP≌△BEP(ASA),
∴PF=PE,DF=BE,
∵四边形ABCD是菱形,
∴GD∥AB,
∴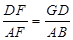 ,
,
∵DF:FA=1:2,
∴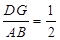 ,
,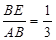 ,
,
∴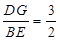 ,
,
∴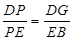 ,即
,即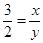 ,
,
∴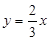 ;
;
②当x=6时,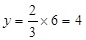 ,
,
∴PF=PE=4,DP=PB=6,
∵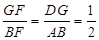 ,
,
∴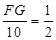 ,
,
解得:FG=5,
故线段FG的长为5.
考点:1.相似三角形的判定与性质;2.全等三角形的判定与性质;3.菱形的性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:计算题
如图D,E分别是△ABC的AB,AC边上的点,且DE∥BC,AD∶AB=1∶4,
(1)证明:△ADE∽△ABC;
(2)当DE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且∠CBF=∠CDB.
(1)求证:FB为⊙O的切线;
(2)若AB=8,CE=2,求sin∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.有下列结论:
①∠DEO=45°;
②△AOD≌△COE;
③S四边形CDOE = S△ABC;
S△ABC;
④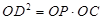 .
.
其中正确的结论序号为 .(把你认为正确的都写上)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图①,将一张矩形纸片对折,然后沿虚线剪切,得到两个(不等边)三角形纸片△ABC,△A1B1C1.
(1)将△ABC,△A1B1C1如图②摆放,使点A1与B重合,点B1在AC边的延长线上,连接CC1交BB1于点E.
①求证:四边形C1B1AB为梯形.
②若∠A="45°," ∠ABC="30°," 求∠B1C1C的度数
(2)若将△ABC,△A1B1C1如图③摆放,使点B1与B重合,点A1在AC边的延长线上,连接CC1交A1B于点F.试判断∠A1C1C与∠A1BC是否相等,并说明理由.
(3)在(2)的条件下,若AC=3,B1C1=6,设A1B=x,C1F=y,写出y与x的函数关系式(不要求写出自变量的取值范围)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN.直线BD与MN相交于E.
(1)如图1,当点M在BC上时,求证:BD-2DE= BM;
BM;
(2)如图2,当点M在BC延长线上时,BD、DE、BM之间满足的关系式是 ;
(3)在(2)的条件下,连接BN交AD于点F,连接MF交BD于点G.若DE= ,且AF:FD=1:2时,求线段DG的长.
,且AF:FD=1:2时,求线段DG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com