
如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且∠CBF=∠CDB.
(1)求证:FB为⊙O的切线;
(2)若AB=8,CE=2,求sin∠F.
(1)见解析;(2)
解析试题分析:(1)连接OB,由圆周角定理可得∠CBD=90°,再由圆所具有的性质及已知条件,可得∠OBF=90°;从而问题得证;
(2)先由垂径定理求得BE的长,然后根据△OBE∽△OBF,利用相似三角形的性质求得OF的长,则sinF即可求解.
试题解析:(1)连接OB.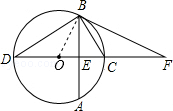
∵CD是直径,
∴∠CBD=90°,
又∵OB=OD,
∴∠OBD=∠D,
又∠CBF=∠D,
∴∠CBF=∠OBD,
∴∠OBF=90°,即OB⊥BF,
∴FB是圆的切线;
(2)∵CD是圆的直径,CD⊥AB,
∴BE= AB=4,
AB=4,
设圆的半径是R,在直角△OEB中,根据勾股定理得:R2=(R﹣2)2+42,
解得:R=5,
∵∠BOE=∠FOB,∠BEO=∠OBF,
∴△OBE∽△OBF,
∴OB2=OE•OF,
∴OF=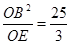 ,
,
则在直角△OBF中,sinF=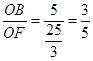
考点:1、圆周角定理;2、切线的判定;3、相似三角形的判定与性质;4、勾股定理


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
已知:如图ΔABC中,D、E、F分别是AB、AC、BC的中点.
(1)若AB=10cm,AC=6cm,则四边形ADFE的周长为______cm
(2)若ΔABC周长为6cm,面积为12cm2,则ΔDEF的周长是 _____,面积是_____
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.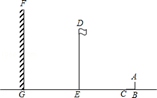
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交边AD于点F,交CD的延长线于点G.
(1)求证:△APB≌△APD;
(2)已知DF∶FA=1∶2,设线段DP的长为x,线段PF的长为y.
①求y与x的函数关系式;
②当x=6时,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在Rt△ABC中,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,
且DM⊥DN,作MF⊥AB于点F,NE⊥AB于点E。
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC。
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,A(-1,1),B(-2,-1).(1)以原点O为位似中心,把线段AB放大到原来的2倍,请在图中画出放大后的线段CD;(2)在(1)的条件下,写出点A的对应点C的坐标为 ,点B的对应点D的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com