
【题目】某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测对在地面A、B两处均探测出建筑物下方C处由生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米,参考数据:sin25°≈0.4,cos25°≈0,9,tan25°≈0.5, ![]() ≈1.7)
≈1.7)
科目:初中数学 来源: 题型:
【题目】八年级某班级部分同学去植树,若每人平均植树7棵,还剩9棵,若每人平均植树9棵,则有1位同学植树的棵数不到8棵.若设同学人数为x人,植树的棵数为(7x+9)棵,下列各项能准确的求出同学人数与种植的树木的数量的是( )
A. 7x+9≤8+9(x﹣1) B. 7x+9≥9(x﹣1)
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
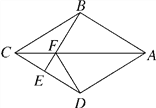
【题目】如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC= ![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.

(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8cm,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.
(1)求证:∠BAC=∠DAC,∠AFD=∠CFE;
(2)若AB∥CD,试证明四边形ABCD是菱形;
(3)在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年某企业按餐厨垃圾处理费25元/ 吨、建筑垃圾处理费16元/ 吨的收费标准,共支付餐厨和建筑垃圾处理费5200元.从2018年元月起,收费标准上调为:餐厨垃圾处理费100元/ 吨,建筑垃圾处理费30元/ 吨.若该企业2018年处理的这两种垃圾数量与2017年相比没有变化,就要多支付垃圾处理费8800元.
(1)该企业2017年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2018年将上述两种垃圾处理总量减少到240吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2018年该企业最少需要支付餐厨垃圾处理费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛.为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,得到分数段在70.5~80.5的频数是50,所占百分比25%,则本次抽样调查的样本容量为_____.
【答案】200
【解析】试题分析:50÷25%=200,
所以本次抽样调查的样本容量是200.
故答案为:200.
【题型】填空题
【结束】
13
【题目】已知P1(x1,y1),P2(x2,y2),P3(x3,y3)是反比例函数![]() 的图象上的三点,且x1<0<x2<x3,则y1,y2,y3的大小关系是________.
的图象上的三点,且x1<0<x2<x3,则y1,y2,y3的大小关系是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com