
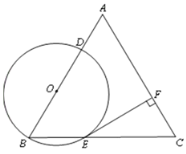
【题目】已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且
分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,某中学准备用长为20m的篱笆围成一个长方形生物园ABCD饲养小兔,生物园的一面靠墙(围墙MN最长可利用15m),设AB长度为x(m),矩形ABCD面积为y(m2).
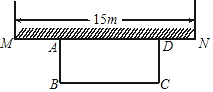
(1)求出y与x的函数关系式,直接写出x的取值范围;
(2)当x为何值时,矩形ABCD的面积最大?最大面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
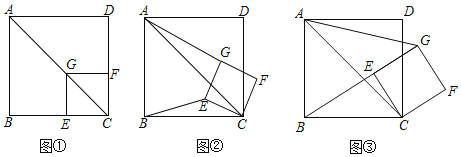
【题目】如图(1),将正方形ABCD与正方形GECF的顶点C重合,当正方形GECF的顶点G在正方形ABCD的对角线AC上时,![]() 的值为______.
的值为______.
如图(2),将正方形CEGF绕点C顺时针方向旋转a角(0°<a<45°),猜测AG与BE之间的数量关系,并说明理由.
如图(3),将正方形CEGF绕点C顺时针方向旋转a角(45°<a<90°)使得B、E、G三点在一条直线上,此时tan∠GAC=![]() ,AG=6,求△BCE的面积.
,AG=6,求△BCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点A(-1,0)和B(0,3),其顶点为D。
轴分别相交于点A(-1,0)和B(0,3),其顶点为D。
(1)求这条抛物线的解析式;
(2)画出此抛物线;
(3)若抛物线与![]() 轴的另一个交点为E,求△ODE的面积;
轴的另一个交点为E,求△ODE的面积;
(4)抛物线的对称轴上是否存在点P使得△PAB的周长最短。若存在请求出点P的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
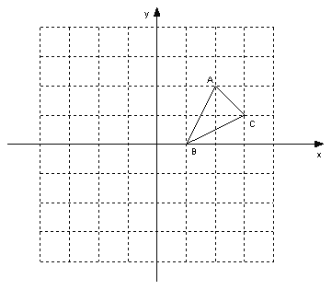
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)画出△ABC关于x轴对称的△A1B1C1,
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2,
(3)△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴并写出对称轴;
(4)△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】箱子里有4瓶牛奶,其中有一瓶是过期的.现从这4瓶牛奶中任意抽取牛奶饮用,抽取任意一瓶都是等可能的.
(1)若小芳任意抽取1瓶,抽到过期的一瓶的概率是 ;
(2)若小芳任意抽取2瓶,请用画树状图或列表法求,抽出的2瓶牛奶中恰好抽到过期牛奶的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
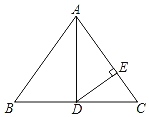
【题目】如图,在△ABC中,AB=AC,AD为边BC上的中线,DE⊥AC于点E.
(1)请你写出图中所有与△CDE相似的三角形;
(2)若AB=10,BC=12,求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点
经过点![]() 和点
和点![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() .
.
(1)求抛物线的解析式;
(2)若点![]() 是抛物线上的动点,点
是抛物线上的动点,点![]() 是抛物线对称轴上的动点,是否存在这样的点
是抛物线对称轴上的动点,是否存在这样的点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,求出点
为顶点的四边形是平行四边形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com