
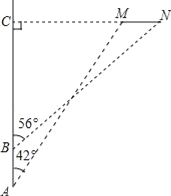
【题目】钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为14.4km(即MC=14.4km).在A点测得岛屿的西端点M在点A的北偏东42°方向;航行4km后到达B点,测得岛屿的东端点N在点B的北偏东56°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离(结果精确到0.1km).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin56°≈0.83,cos56°≈0.56,tan56°≈1.48)
科目:初中数学 来源: 题型:
【题目】若等腰三角形的两边长分别是6cm和4cm,则等腰三角形的周长是( )
A. 16cm B. 14cm C. 16cm或14cm D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题: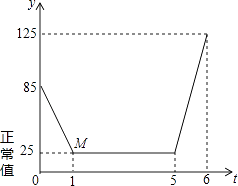
(1)写出题中的变量;
(2)写出点M的实际意义;
(3)求第1小时内,y与t的一次函数表达式;
(4)已知第5﹣6小时是小强妈妈做晚餐的时间,厨房内油烟导致PM2.5浓度升高.若该净化器吸收PM2.5的速度始终不变,则第6小时之后,预计经过多长时间室内PM2.5浓度可恢复正常?
查看答案和解析>>
科目:初中数学 来源: 题型:
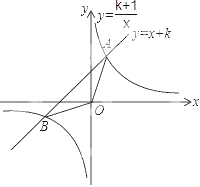
【题目】如图,已知直线![]() 和双曲线
和双曲线![]() (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点.
(1)当k=1时,求A、B两点的坐标;
(2)当k=2时,求△AOB的面积;
(3)当k=1时,△OAB的面积记为S1,当k=2时,△OAB的面积记为S2,…,依此类推,当k=n时,△OAB的面积记为Sn,若S1+S2+…+Sn=![]() ,求n的值.
,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com