
【题目】如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,则∠EOF的度数是( )

A. 88° B. 30° C. 32° D. 48°
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
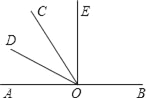
【题目】如图,O是直线AB上一点,OD平分∠AOC.
(1)若∠AOC=60°,请求出∠AOD和∠BOC的度数.
(2)若∠AOD和∠DOE互余,且∠AOD=![]() ∠AOE,请求出∠AOD和∠COE的度数.
∠AOE,请求出∠AOD和∠COE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( ) 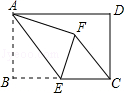
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=3cm,现将纸片折叠压平,使点A与点C重合,折痕为EF,如果sin∠BAE= ![]() ,那么重叠部分△AEF的面积为( )
,那么重叠部分△AEF的面积为( ) 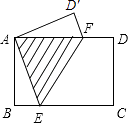
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)3![]() ﹣5
﹣5![]() ﹣(﹣1
﹣(﹣1![]() )﹣3
)﹣3![]() +12
+12![]() ﹣(﹣12
﹣(﹣12![]() )
)
(2)|﹣![]() |×[﹣32÷(﹣
|×[﹣32÷(﹣![]() )2+(﹣2)3]
)2+(﹣2)3]
(3)先化简,再求值:2x2﹣[3(﹣![]() x2+
x2+![]() xy)﹣2y2]﹣2(x2﹣xy+2y2),其中x、y满足|x﹣
xy)﹣2y2]﹣2(x2﹣xy+2y2),其中x、y满足|x﹣![]() |+(y+1)2=0.
|+(y+1)2=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的象经过A(﹣1,0)、B(3,0)、N(2,3)三点,且与y轴交于点C.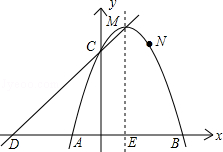
(1)求这个二次函数的解析式,并写出顶点M及点C的坐标;
(2)若直线y=kx+d经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;
(3)点P是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P,使以点P为圆心的圆经过A、B两点,并且与直线CD相切?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题: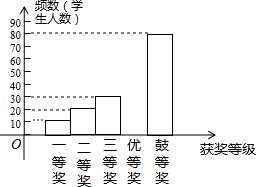
(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com