
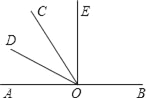
【题目】如图,O是直线AB上一点,OD平分∠AOC.
(1)若∠AOC=60°,请求出∠AOD和∠BOC的度数.
(2)若∠AOD和∠DOE互余,且∠AOD=![]() ∠AOE,请求出∠AOD和∠COE的度数.
∠AOE,请求出∠AOD和∠COE的度数.
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是( ) 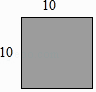
A.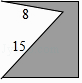
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空或填写理由.
(1)如图甲,∵∠ =∠ (已知);
∴AB∥CD( )
(2)如图乙,已知直线a∥b,∠3=80°,求∠1,∠2的度数.
解:∵a∥b,( )
∴∠1=∠4( )
又∵∠3=∠4( )
∠3=80°(已知)
∴∠1=( )(等量代换)
又∵∠2+∠3=180°
∴∠2=( )(等式的性质)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y1=x+m的图象与反比例函数y2= ![]() 的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2 .
的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2 .
(1)求一次函数的函数表达式;
(2)已知反比例函数在第一象限的图象上有一点C到x轴的距离为2,求△ABC的面积. 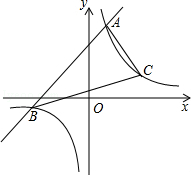
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:①∠1是∠B的余角;②图中互余的角共有3对;③∠1的补角只有∠ACF;④与∠ADB互补的角共有3个.则上述结论正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距720km,一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是120km/h,慢车的速度是80km/h,快车到达乙地后,停留了20min,由于有新的任务,于是立即按原速返回甲地.在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,这两次相遇时间间隔是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A在射线CE上,∠C=∠D.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,则∠EOF的度数是( )

A. 88° B. 30° C. 32° D. 48°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com