
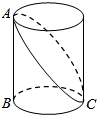
 如图,已知圆柱底面的周长为4分米,圆柱高为2分米,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的长度最短为
如图,已知圆柱底面的周长为4分米,圆柱高为2分米,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的长度最短为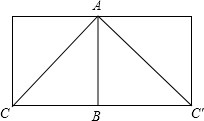 解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
 如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )| A、两点之间线段最短 |
| B、两点确定一条直线 |
| C、垂线段最短 |
| D、以上都不是 |
查看答案和解析>>
科目:初中数学 来源: 题型:
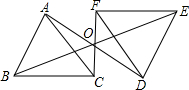 如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )
如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )| A、点A与点D是对应点 |
| B、BO=EO |
| C、∠ACB=∠FDE |
| D、AB∥DE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com