练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】将一些完全相同的正三角形按如图所示规律摆放，第一个图形有1个正三角形，第二个图形有5个正三角形，第三个图形有12个正三角形，…，按此规律排列下去，第六个图形中正三角形的个数是（　　）

    A. 35 B. 41 C. 45 D. 51

    【答案】D

    【解析】

    观察图形发现：第一个图形有1=1个正三角形，第二个图形有1+2+2=5个正三角形，第三个图有1+2+3+2+4=12个正三角形，第四个图有1+2+3+4+2+4+6=22个正三角形，由此可知第n 个图形中有1+2+3+…+n+2+4+…+2（n-1）=，由此进行计算即可得.

    观察图形发现：

    第一个图形有1=1个正三角形，

    第二个图形有1+2+2=5个正三角形，

    第三个图有1+2+3+2+4=12个正三角形，

    第四个图有1+2+3+4+2+4+6=22个正三角形，

    …

    ∴第n 个图形中有1+2+3+…+n+2+4+…+2（n-1）= ，

    n=6时，=51，

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】BD、CE分别是△ABC的边AC、AB上的高，P在BD的延长线上，且BP=AC，点Q在CE上，CQ=AB,

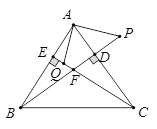
    求证：（1）AP=AQ ；

    （2）AP⊥AQ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将△ABC纸片沿DE折叠，使点A落在点A′处，且A′B平分∠ABC，A′C平分∠ACB，若∠BA′C=110°，则∠1+∠2=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB＝BC，∠ABC＝45°，BE⊥AC于点E，AD⊥BC于点D，BE与AD相交于F．

    （1）求证：BF＝AC；

    （2）若BF＝3，求CE的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB=AC≠BC，点D和点A在直线BC的同侧，BD=BC，∠BAC=α，∠DBC=β，且α+β=120°，连接AD，求∠ADB的度数．（不必解答）

    （1）小聪先从特殊问题开始研究，当α=90°，β=30°时，利用轴对称知识，以AB为对称轴构造△ABD的轴对称图形△ABD′，连接CD′（如图2），然后利用α=90°，β=30°以及等边三角形等相关知识便可解决这个问题．

    请结合小聪研究问题的过程和思路，在这种特殊情况下填空：△D′BC的形状是　 　三角形；∠ADB的度数为　 　．

    （2）在原问题中，当∠DBC＜∠ABC（如图1）时，请计算∠ADB的度数；

    （3）在原问题中，过点A作直线AE⊥BD，交直线BD于E，其他条件不变若BC=7，AD=2．请直接写出线段BE的长为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知A地在C、B两地之间，甲乙两人分别从A、B两地同时出发，相向而行，经过一段时间后相遇，甲继续向B地前进，乙继续向A地前进；甲到达B地后立即返回，在C地甲追上乙．甲乙两人相距的路程y（米）与出发的时间x（分钟）之间的关系如图所示，则A、C两地相距___米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一列动车从甲地开往乙地，一列普通列车从乙地开往甲地，两车同时出发，设普通列车行驶的时间为（小时），两车之间的距离为（千米），图中的折线表示与之间的函数关系。

    根据图象回答下列问题：

    （1）甲地与乙地相距______千米，两车出发后______小时相遇；

    （2）普通列车到达终点共需_______小时，普通列车的速度是______千米/小时；

    （3）动车的速度是________千米/小时；

    （4）的值为________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形ABCD中，AB=3，AD=6，点E是边AD上的一个动点，把△BAE沿BE折叠，若点A的对应点A′恰落在矩形ABCD的对称轴上，则AE=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

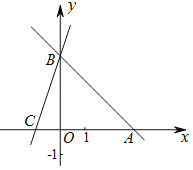
    【题目】如图，直线y＝﹣x+b分别与x轴、y轴交于A，B两点，点A的坐标为（3，0），过点B的另一条直线交x轴负半轴于点C，且OB：OC＝3：1．

    （1）求点B的坐标及直线BC对应的函数表达式；

    （2）在线段OB上存在点P，使得点P到点B，C的距离相等，试求出点P的坐标；

    （3）如果在x轴上方存在点D，使得以点A，B，D为顶点的三角形与△ABC全等，请直接写出点D的坐标．

    查看答案和解析>>

    同步练习册答案