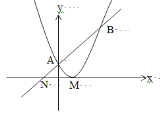
【题目】已知抛物线y=
（b<0）的图像的顶点为 M，与 y 轴交于点 A，过点 A的直线 y=x+c 与 x 轴交于点 N，与抛物线另交于点B（6，8）.
（1）求线段 AN 的长；
（3）平移该抛物线得到一条新抛物线.设新抛物线的顶点为 M’.若新抛物线经过点 N,， 且新抛物线的顶点和原抛物线的顶点的连线 MM’平行于直线 AB，求新抛物线对应的函数表达式.
【答案】（1）
.（2）答案见解析.
【解析】
（1）根据点的坐标先求出函数解析式，再求出A点和N点（2）根据抛物线的平移先设解析式，求出点的坐标，再求抛物线的解析式.
解：（1）直线
与抛物线y=
相交与A点和B点
已知点B（6,8），将点B带入直线解析式中得：
直线解析式为
点坐标（-2,0），
点坐标（0,2）
（2）由（1）知，点坐标（0,2），点B（6,8）
带入抛物线解析式中得：
抛物线解析式为y=
当y等于0时得：
顶点M的坐标为（2,0）
设新抛物线的顶点为 M’.若新抛物线经过点 N,， 且新抛物线的顶点和原抛物线的顶点的连线 MM’平行于直线 AB
经过MM’的直线解析式为
设新抛物线函数解析式为
经过MM’的直线解析式为
新抛物线的函数表达式为：
或
.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
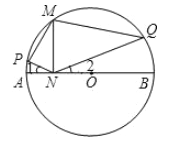
【题目】如图，
是⊙
的直径，
是⊙上一点，
，垂足为
、
、
分别是
、
上一点（不与端点重合），如果
，下面结论：①
；②
；③
；④
；⑤
．其中正确的是（ ）
A. ①②③B. ①③⑤C. ④⑤D. ①②⑤
查看答案和解析>>
科目：初中数学 来源： 题型：
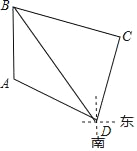
【题目】分别静止在A、B处（B在A的正北方）是我国两艘军舰相距10km，为在D处的一艘我国货轮执行护航任务，A处军舰测得D点在南偏东63.4°，B处军舰测得D点在南偏东36.8°．货轮沿着北偏东16.4°方向航行了12km到达C点，此时在B处的军舰测得C点在南偏东73.6°方向上．
（1）求∠BCD的度数；
（2）求AD的长．（参考数据：sin36.8°≈0.60，cos36.8°≈0.80，tan26.6°≈0.50，
≈2.24）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某文具店购进一批纪念册，每本进价为20元，出于营销考虑，要求每本纪念册的售价不低于20元且不高于28元，在销售过程中发现该纪念册每周的销售量y（本）与每本纪念册的售价x（元）之间满足一次函数关系：当销售单价为22元时，销售量为36本；当销售单价为24元时，销售量为32本．
（1）求出y与x的函数关系式；
（2）当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是多少元？
（3）设该文具店每周销售这种纪念册所获得的利润为w元，将该纪念册销售单价定为多少元时，才能使文具店销售该纪念册所获利润最大？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
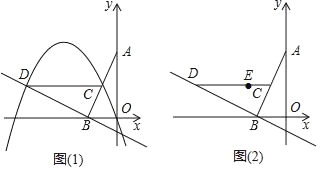
【题目】已知在平面直角坐标系xOy中，O为坐标原点，线段AB的两个端点的坐标分别为A （0，2），B（﹣1，0），点C为线段AB的中点，现将线段BA绕点B按逆时针方向旋转90°得到线段BD，抛物线y＝ax2+bx+c（a≠0）、经过点D．
(1)如图1，若该抛物线经过原点O，且a＝﹣1．
①求点D的坐标及该抛物线的解析式；
②连结CD，问：在抛物线上是否存在点P，使得∠POB与∠BCD互余？若存在，请求出所有满足条件的点P的坐标，若不存在，请说明理由．
(2)如图2，若该抛物线y＝ax2+bx+c（a＜0）经过点E（﹣1，1），点Q在抛物线上，且满足∠QOB与∠BCD互余，若符合条件的Q点的个数是4个，请直接写出a的取值范围 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“食品安全”受到全社会的广泛关注，济南市某中学对部分学生就食品安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两份尚不完整的统计图，请你根据统计图中所提供的信息解答下列问题.
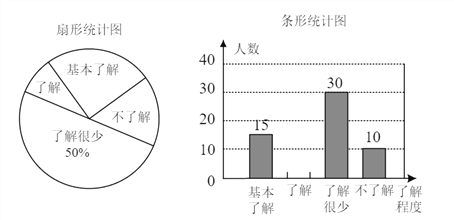
（1）接受问卷调查的学生共有_____人，扇形统计图中“基本了解”部分所对应扇形的圆心角为_____.
（2）请补全条形统计图.
（3）若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数.
（4）若从对食品安全知识达到“了解”程度的2个女生和2个男生中随机抽取2人参加食品安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
【答案】（1）60；90°；（2）补图见解析；（3）300；（4）
【解析】分析：（1）根据了解很少的人数除以了解很少的人数所占的百分百求出抽查的总人数，再用“基本了解”所占的百分比乘以360°，即可求出“基本了解”部分所对应扇形的圆心角的度数；（2）用调查的总人数减去“基本了解”“了解很少”和“基本了解”的人数，求出了解的人数，从而补全统计图；（3）用总人数乘以“了解”和“基本了解”程度的人数所占的比例，即可求出达到“了解”和“基本了解”程度的总人数；（4）根据题意列出表格，再根据概率公式即可得出答案．
详解：（1）60；90°.
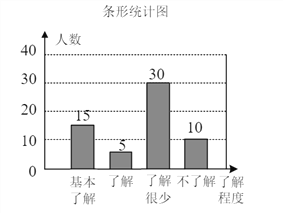
（2）补全的条形统计图如图所示.
（3）对食品安全知识达到“了解”和“基本了解”的学生所占比例为
，由样本估计总体，该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数为
.
（4）列表法如表所示，
男生 | 男生 | 女生 | 女生 | |
男生 | 男生男生 | 男生女生 | 男生女生 | |
男生 | 男生男生 | 男生女生 | 男生女生 | |
女生 | 男生女生 | 男生女生 | 女生女生 | |
女生 | 男生女生 | 女生女生 |
所有等可能的情况一共12种，其中选中1个男生和1个女生的情况有8种，所以恰好选中1个男生和1个女生的概率是
.
点睛：本题考查了条形统计图、扇形统计图以及用列表法或树状图法求概率，根据题意求出总人数是解题的关键；注意运用概率公式：概率=所求情况数与总情况数之比．
【题型】解答题
【结束】
24
【题目】为响应国家全民阅读的号召，某社区鼓励居民到社区阅览室借阅读书，并统计每年的借阅人数和图书借阅总量（单位：本），该阅览室在2015年图书借阅总量是7500本，2017年图书借阅总量是10800本.
（1）求该社区的图书借阅总量从2015年至2017年的年平均增长率.
（2）已知2017年该社区居民借阅图书人数有1350人，预计2018年达到1440人，如果2017年至2018年图书借阅总量的增长率不低于2015年至2017年的年平均增长率，设2018年的人均借阅量比2017年增长a%，求a的值至少是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
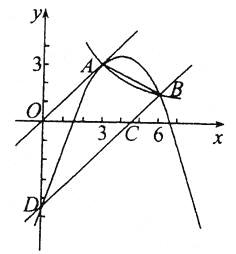
【题目】如图，正比例函数和反比例函数的图象都经过点 A ( 3 , 3) ，把直线 OA 向下平移后，与反比例函数的图象交于点B(6,m)，与x轴、y轴分别交于C、D两点.
(1）求 m的值；
( 2 ）求过 A、B、D 三点的抛物线的解析式；
( 3 ）若点E是抛物线上的一个动点，是否存在点 E，使四边形 OECD 的面积S1，是四边形OACD 面积S的
?若存在，求点 E 的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，以AC为直径作⊙O交BC于点D，交AB于点G，且D是BC中点，DE⊥AB，垂足为E，交AC的延长线于点F．
（1）求证：直线EF是⊙O的切线；
（2）若CF=3，cosA=0.4，求出⊙O的半径和BE的长；
（3）连接CG，在（2）的条件下，求CG:EF的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
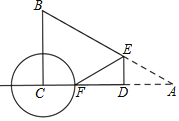
【题目】如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=4
．若动点D在线段AC上（不与点A、C重合），过点D作DE⊥AC交AB边于点E．点A关于点D的对称点为点F，以FC为半径作⊙C，当DE=_______时，⊙C与直线AB相切．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com