
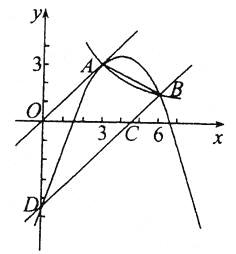
【题目】如图,正比例函数和反比例函数的图象都经过点 A ( 3 , 3) ,把直线 OA 向下平移后,与反比例函数的图象交于点B(6,m),与x轴、y轴分别交于C、D两点.
(1)求 m的值;
( 2 )求过 A、B、D 三点的抛物线的解析式;
( 3 )若点E是抛物线上的一个动点,是否存在点 E,使四边形 OECD 的面积S1,是四边形OACD 面积S的![]() ?若存在,求点 E 的坐标;若不存在,请说明理由.
?若存在,求点 E 的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)抛物线的解析式为
;(2)抛物线的解析式为![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)由于反比例函数的图象都经过点A(3,3),由此可以确定函数的解析式,又把直线OA向下平移后,与反比例函数的图象交于点B(6,m),把B的坐标代入反比例函数的解析式即可确定m的值;
(2)由于直线OA向下平移后,与反比例函数的图象交于点B(6,m),与x轴、y轴分别交于C、D两点,由此首先确定直线BD的解析式,接着可以确定C,D的坐标,最后利用待定系数法即可确定过A、B、D三点的抛物线的解析式;
(3)如图,利用(1)(2)知道四边形OACD是梯形,利用已知条件可以求出其面积,设E的横坐标为x,那么利用x可以表示其纵坐标,也可以表示△OEC的面积,而△OCD的面积可以求出,所以根据四边形OECD的面积S1,是四边形OACD面积S的![]() 即可列出关于x的方程,利用方程即可解决问题.
即可列出关于x的方程,利用方程即可解决问题.
(1)∵反比例函数的图象都经过点A(3,3),
∴经过点A的反比例函数解析式为:y=![]() ,
,
而直线OA向下平移后,与反比例函数的图象交于点B(6,m),
∴m=![]() ;
;
(2)∵直线OA向下平移后,与反比例函数的图象交于点B(6,![]() ),
),
与x轴、y轴分别交于C、D两点,
而这些OA的解析式为y=x,
设直线CD的解析式为y=x+b,
代入B的坐标得:![]() =6+b,
=6+b,
∴b=-4.5,
∴直线OC的解析式为y=x-4.5,
∴C、D的坐标分别为(4.5,0),(0,-4.5),
设过A、B、D三点的抛物线的解析式为y=ax2+bx+c,
分别把A、B、D的坐标代入其中得:
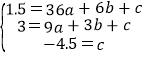 ,
,
解之得:a=-0.5,b=4,c=-4.5
∴y=-![]() x2+4x-
x2+4x-![]() ;
;
(3)如图,设E的横坐标为x,
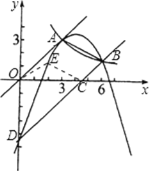
∴其纵坐标为-0.5x2+4x-4.5,
∴S1=![]() (-0.5x2+4x-4.5+OD)×OC,
(-0.5x2+4x-4.5+OD)×OC,
=![]() (-0.5x2+4x-4.5+4.5)×4.5,
(-0.5x2+4x-4.5+4.5)×4.5,
=![]() (-0.5x2+4x)×4.5,
(-0.5x2+4x)×4.5,
而S=![]() (3+OD)×OC=
(3+OD)×OC=![]() (3+4.5)×4.5=
(3+4.5)×4.5=![]() ,
,
∴![]() (-0.5x2+4x)×4.5=
(-0.5x2+4x)×4.5=![]() ×
×![]() ,
,
解之得x=4±![]() ,
,
∴这样的E点存在,坐标为(4-![]() ,
,![]() ),(4+
),(4+![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】复习课中,教师给出关于x的函数![]() (k是实数).
(k是实数).
教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写到黑板上.
学生思考后,黑板上出现了一些结论.教师作为活动一员,又补充一些结论,并从中选择如下四条:
①存在函数,其图像经过(1,0)点;
②函数图像与坐标轴总有三个不同的交点;
③当![]() 时,不是y随x的增大而增大就是y随x的增大而减小;
时,不是y随x的增大而增大就是y随x的增大而减小;
④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数;
教师:请你分别判断四条结论的真假,并给出理由,最后简单写出解决问题时所用的数学方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△ABC向上平移3个单位长度,画出平移后的△A1B1C1;
(2)写出A1、C1的坐标;
(3)将△A1B1C1绕B1逆时针旋转90°,画出旋转后的△A2B1C2,求线段B1C1旋转过程中扫过的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
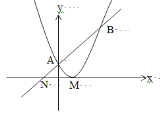
【题目】已知抛物线y=![]() (b<0)的图像的顶点为 M,与 y 轴交于点 A,过点 A的直线 y=x+c 与 x 轴交于点 N,与抛物线另交于点B(6,8).
(b<0)的图像的顶点为 M,与 y 轴交于点 A,过点 A的直线 y=x+c 与 x 轴交于点 N,与抛物线另交于点B(6,8).
(1)求线段 AN 的长;
(3)平移该抛物线得到一条新抛物线.设新抛物线的顶点为 M’.若新抛物线经过点 N,, 且新抛物线的顶点和原抛物线的顶点的连线 MM’平行于直线 AB,求新抛物线对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题是( )

A. ①② B. ②③ C. ①③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
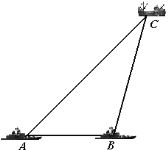
【题目】如图,在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持10海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一不明国籍的渔船C,求此时渔船C与海监船B的距离是多少.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;(2)若CD=1,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省温州市)如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数![]() (k≠0)的图象恰好经过点A′,B,则k的值为______.
(k≠0)的图象恰好经过点A′,B,则k的值为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com