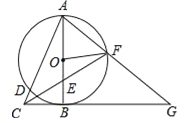
【题目】如图，以Rt△ABC的直角边AB为直径作⊙O，交斜边AC于点D，点E为OB的中点，连接CE并延长交⊙O于点F，点F恰好落在的中点，连接AF并延长与CB的延长线相交于点G，连接OF．

（1）求证：OF=BG；

（2）若AB=4，求DC的长．

参考答案：

【答案】（1）证明见解析；（2）．

【解析】

试题分析：（1）直接利用圆周角定理结合平行线的判定方法得出FO是△ABG的中位线，即可得出答案；

（2）首选得出△FOE≌△CBE（ASA），则BC=FO=AB=2，进而得出AC的长，再利用相似三角形的判定与性质得出DC的长．

试题解析：（1）证明：∵以Rt△ABC的直角边AB为直径作⊙O，点F恰好落在的中点，∴，∴∠AOF=∠BOF，∵∠ABC=∠ABG=90°，∴∠AOF=∠ABG，∴FO∥BG，∵AO=BO，∴FO是△ABG的中位线，∴FO=BG；

（2）解：在△FOE和△CBE中，∵∠FOE=∠CBE，EO=BE，∠OEF=∠CEB，∴△FOE≌△CBE（ASA），∴BC=FO=AB=2，∴AC==，连接DB，∵AB为⊙O直径，∴∠ADB=90°，∴∠ADB=∠ABC，∵∠BCD=∠ACB，∴△BCD∽△ACB，∴，∴，解得：DC=．

关闭