
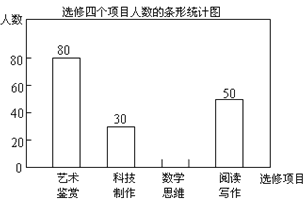
【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”,“科技制作”,“数学思维”,“阅读写作”这四个选修项目的学生(每人限报一课)进行抽样调查,下面是根据收集的数据绘制的不完整的统计图:
请根据图中提供的信息,解答下面的问题:
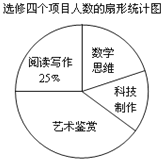
(1)此次共调查了___名学生,扇形统计图中“艺术鉴赏”部分的圆心角是___度;
(2)此次调查“数学思维”的人数为_________,并补充完整条形图;
(3)现该校共有600名学生报名参加这四个选修项目,请你估计其中有____名学生选修“科技制作”项目.
【答案】(1)200;144;(2)40名;(3)90.
【解析】
(1)由所给统计图中的信息可知,选修“阅读写作”的有50人,占被调查人数的25%,由此可得被调查人数为:50÷25%=200(人);结合选修“艺术鉴赏”的人数为80人即可计算出扇形统计图中“艺术鉴赏”所占的百分比,由此即可计算出扇形统计图中“艺术鉴赏”部分的圆心角的度数了;
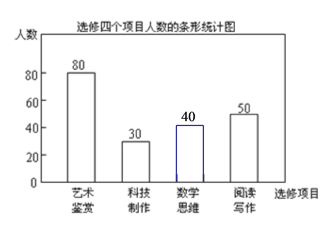
(2)由(1)中所得结果和条形统计图中的信息可得:选修“数学思维”的人数为:200-80-30-50=40(人),根据所得数据再将条形统计图补充完整即可;
(3)根据(1)中所得结果结合已知条件计算出选修“科技制作”的人数占被调查人数的百分比,再用600乘以所得的百分比即可求出全校选修“科技制作”的人数了.
(1)根据题意得:被调查的学生总数是:50÷25%=200(名),
∵被调查的学生中,选修“艺术鉴赏”的有80人,
∴扇形统计图中,“艺术鉴赏”部分的圆心角=![]() ×360°=144°;
×360°=144°;
故答案为:200,144;
(2)由统计图中所给信息和(1)中所得被调查总人数为200人可得:
选修“数学思维”的人数是:200-80-30-50=40(名),
将条形统计图补充完整如下:
(3)根据题意得:全校600名报了“选修课”的学生中选修“科技制作”的人数约为600×![]() =90(名),
=90(名),
答:其中有90名学生选修“科技制作”项目.


科目:初中数学 来源: 题型:
【题目】如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.
![]()
(1)请写出与A,B两点距离相等的点M所对应的数 .
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,x秒后两只电子蚂蚁在数轴上的C点相遇,请列方程求出x,并指出点C表示的数.
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,y秒后两只电子蚂蚁在数轴上的D点相遇,请列方程求出y并指出点D表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AD是弦,∠A=22.5°,延长AB到点C,使得∠ACD=45°. 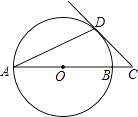
(1)求证:CD是⊙O的切线.
(2)若AB=2 ![]() ,求OC的长.
,求OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学八年级的篮球队有![]() 名队员.在罚篮投球训练中,这
名队员.在罚篮投球训练中,这![]() 名队员各投篮
名队员各投篮![]() 次的进球情况如下表:
次的进球情况如下表:
进球数 |
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
针对这次训练,请解答下列问题:
![]() 这
这![]() 名队员进球数的平均数是________,中位数是________;
名队员进球数的平均数是________,中位数是________;
![]() 求这支球队罚篮命中率.罚篮命中率
求这支球队罚篮命中率.罚篮命中率![]() (进球数
(进球数![]() 投篮次数)
投篮次数)![]() ________;
________;
![]() 若队员小亮的罚篮命中率为
若队员小亮的罚篮命中率为![]() ,请你分析小亮在这支球队中的罚篮水平.
,请你分析小亮在这支球队中的罚篮水平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:在数学课上,老师提出如下问题:
尺规作图,过圆外一点作圆的切线. |
小涵的主要作法如下:
如图,(1)连结OP,作线段OP的中点A; |
老师说:“小涵的做法是正确的.”
请回答:小涵的作图依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E. 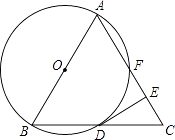
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )

A. ①②④ B. ②③④
C. ①②③ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com