
【题目】如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
A.
B.
C.
D.
【答案】B
【解析】解:根据题意BE=CF=t,CE=8﹣t,
∵四边形ABCD为正方形,
∴OB=OC,∠OBC=∠OCD=45°,
∵在△OBE和△OCF中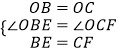 ,
,
∴△OBE≌△OCF(SAS),
∴S△OBE=S△OCF ,
∴S四边形OECF=S△OBC= ![]() ×82=16,
×82=16,
∴S=S四边形OECF﹣S△CEF=16﹣ ![]() (8﹣t)t=
(8﹣t)t= ![]() t2﹣4t+16=
t2﹣4t+16= ![]() (t﹣4)2+8(0≤t≤8),
(t﹣4)2+8(0≤t≤8),
∴s(cm2)与t(s)的函数图象为抛物线一部分,顶点为(4,8),自变量为0≤t≤8.
故选:B.
由点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,得到BE=CF=t,则CE=8﹣t,再根据正方形的性质得OB=OC,∠OBC=∠OCD=45°,然后根据“SAS”可判断△OBE≌△OCF,所以S△OBE=S△OCF , 这样S四边形OECF=S△OBC=16,于是S=S四边形OECF﹣S△CEF=16﹣ ![]() (8﹣t)t,然后配方得到S=
(8﹣t)t,然后配方得到S= ![]() (t﹣4)2+8(0≤t≤8),最后利用解析式和二次函数的性质对各选项进行判断.
(t﹣4)2+8(0≤t≤8),最后利用解析式和二次函数的性质对各选项进行判断.


科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m厘米,宽为n厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )

A. 4m厘米 B. 4n厘米 C. 2(m+n)厘米 D. 4(m-n)厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
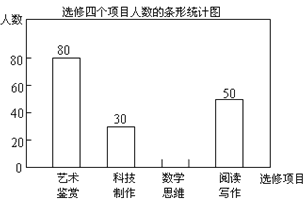
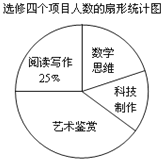
【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”,“科技制作”,“数学思维”,“阅读写作”这四个选修项目的学生(每人限报一课)进行抽样调查,下面是根据收集的数据绘制的不完整的统计图:
请根据图中提供的信息,解答下面的问题:
(1)此次共调查了___名学生,扇形统计图中“艺术鉴赏”部分的圆心角是___度;
(2)此次调查“数学思维”的人数为_________,并补充完整条形图;
(3)现该校共有600名学生报名参加这四个选修项目,请你估计其中有____名学生选修“科技制作”项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1。在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换。若骰子的初始位置为图1所示的状态,那么按上述规则连续完成14次变换后,骰子朝上一面的点数是_____________________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近两年,国际市场黄金价格涨幅较大,中国交通银行推出“沃德金”的理财产品,即以黄金为投资产品,投资者从黄金价格的上涨中赚取利润.上周五黄金的收盘价为![]() 元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六、星期日休市)
元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六、星期日休市)
星期 | 一 | 二 | 三 | 四 | 五 |
收盘价的变化(与前一天收盘价比较) |
|
|
|
|
|
问
![]() 本周星期三黄金的收盘价是多少?
本周星期三黄金的收盘价是多少?
![]() 本周黄金收盘时的最高价、最低价分别是多少?
本周黄金收盘时的最高价、最低价分别是多少?
![]() 上周,小王以周五的收盘价
上周,小王以周五的收盘价![]() 元/克买入黄金
元/克买入黄金![]() 克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金
克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金![]() 克,他的收益情况如何?
克,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是AB上一点,DF交AC于点E,FC∥AB,则下列结论错误的是( )

A. 若AE=CE,则DE=FE B. 若DE=FE,则AE=CE
C. 若BC=CF,则AD=CF D. 若AD=CF,则DE=FE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答问题.
饮水问题是关系到学生身心健康的重要生活环节,东坡中学共有教学班24个,平均每班有学生50人,经估算,学生一年在校时间约为240天(除去各种节假日),春、夏、秋、冬季各60天.原来,学生饮水一般都是购纯净水(其他碳酸饮料或果汁价格更高),纯净水零售价为1.5元/瓶,每个学生春、秋、冬季平均每天买1瓶纯净水,夏季平均每天要买2瓶纯净水,学校为了减轻学生消费负担,要求每个班自行购买1台冷热饮水机,经调查,购买一台功率为500 W的冷热饮水机约为150元,纯净水每桶6元,每班春、秋两季,平均每1.5天购买4桶,夏季平均每天购买5桶,冬季平均每天购买1桶,饮水机每天开10小时,当地民用电价为0.50元/度.
问题:
(1)在未购买饮水机之前,全年平均每个学生要花费多少钱来购买纯净水饮用?
(2)在购买饮水机解决学生饮水问题后,每班当年共要花费多少元?
(3)这项便利学生的措施实施后,东坡中学当年全体学生共节约多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】88层的金茂大厦的电梯上,有显示楼层的液晶屏,如图,可显示01,02,…,88,由于屏幕受到损坏,显示左边数字的7根线段中有1根不能亮了,显示右边数字的7根线段中有3根不能亮了。请问:电梯在运行的过程中,最多还有 _____个楼层的数字显示是正确的.

(说明)数字0、1、2、3、4、5、6、7、8、9显示方式如下图所示.

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论:w
①若a+b+c=0,且abc≠0,则方程a+bx+c=0的解是x=1;
②若a(x﹣1)=b(x﹣1)有唯一的解,则a≠b;
③若b=2a,则关于x的方程ax+b=0(a≠0)的解为x=﹣![]() ;
;
④若a+b+c=1,且a≠0,则x=1一定是方程ax+b+c=1的解;
其中结论正确个数有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com