【题目】将正方体骰子（相对面上的点数分别为1和6、2和5、3和4）放置于水平桌面上，如图1。在图2中，将骰子向右翻滚90°，然后在桌面上按逆时针方向旋转90°，则完成一次变换。若骰子的初始位置为图1所示的状态，那么按上述规则连续完成14次变换后，骰子朝上一面的点数是_____________________。
科目：初中数学 来源： 题型：
【题目】如图所示，已知AB是圆O的直径，圆O过BC的中点D，且DE⊥AC．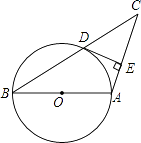 
（1）求证：DE是圆O的切线；
（2）若∠C=30°，CD=10cm，求圆O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学八年级的篮球队有
名队员．在罚篮投球训练中，这名队员各投篮
次的进球情况如下表：
进球数 |
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
针对这次训练，请解答下列问题：
这名队员进球数的平均数是________，中位数是________；
求这支球队罚篮命中率．罚篮命中率
（进球数
投篮次数）
________；
若队员小亮的罚篮命中率为
，请你分析小亮在这支球队中的罚篮水平．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，BD垂直平分AC，垂足为点F，E为四边形ABCD外一点，且∠ADE=∠BAD，AE⊥AC．
（1）求证：四边形ABDE是平行四边形；
（2）如果DA平分∠BDE，AB=5，AD=6，求AC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC是等边三角形，以AB为直径作⊙O，交BC边于点D，交AC边于点F，作DE⊥AC于点E．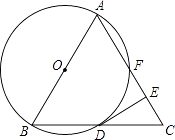 
（1）求证：DE是⊙O的切线；
（2）若△ABC的边长为4，求EF的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知数轴上点A表示的数为6，B是数轴上一点，且AB=10，动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒，
（1）写出数轴上点B所表示的数 ；
（2）点P所表示的数 ；（用含t的代数式表示）；
（3）M是AP的中点，N为PB的中点，点P在运动的过程中，线段MN的长度是否发生变化？若变化，说明理由；若不变，请你画出图形，并求出线段MN的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，AB=8cm，对角线AC，BD相交于点O，点E，F分别从B，C两点同时出发，以1cm/s的速度沿BC，CD运动，到点C，D时停止运动，设运动时间为t（s），△OEF的面积为s（cm2），则s（cm2）与t（s）的函数关系可用图象表示为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在求1+2+22+23+24+25+26的值时，小明发现：从第二个加数起每一个加数都是前一个加数的2倍，于是他设：S=1+2+22+23+24+25+26①然后在①式的两边都乘以2，得：2S=2+22+23+24+25+26+27 ②；②﹣①得2S﹣S=27﹣1，S=27﹣1，即1+2+22+23+24+25+26=27﹣1．
（1）求1+3+32+33+34+35+36的值；
（2）求1+a+a2+a3+…+a2013（a≠0且a≠1）的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，⊙C的半径为r，P是与圆心C不重合的点，点P关于⊙C的限距点的定义如下：若P′为直线PC与⊙C的一个交点，满足r≤PP′≤2r，则称P′为点P关于⊙C的限距点，如图为点P及其关于⊙C的限距点P′的示意图． 
（1）当⊙O的半径为1时．
①分别判断点M（3，4），N（ 
，0），T（1， 
）关于⊙O的限距点是否存在？若存在，求其坐标；
②点D的坐标为（2，0），DE，DF分别切⊙O于点E，点F，点P在△DEF的边上．若点P关于⊙O的限距点P′存在，求点P′的横坐标的取值范围；
（2）保持（1）中D，E，F三点不变，点P在△DEF的边上沿E→F→D→E的方向运动，⊙C的圆心C的坐标为（1，0），半径为r，请从下面两个问题中任选一个作答．
问题1 | 问题2 |
若点P关于⊙C的限距点P′存在，且P′随点P的运动所形成的路径长为πr，则r的最小值为 | 若点P关于⊙C的限距点P′不存在，则r的取值范围为 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
