
【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E. 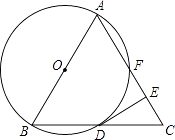
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
【答案】
(1)证明:如图1,连接OD,
∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵OB=OD,
∴∠ODB=∠B=60°.
∵DE⊥AC,
∴∠DEC=90°.
∴∠EDC=30°.
∴∠ODE=90°.
∴DE⊥OD于点D.
∵点D在⊙O上,
∴DE是⊙O的切线
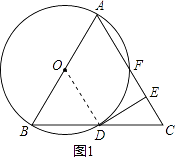
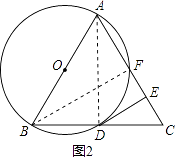
(2)解:如图2,连接AD,BF,
∵AB为⊙O直径,
∴∠AFB=∠ADB=90°.
∴AF⊥BF,AD⊥BD.
∵△ABC是等边三角形,
∴ ![]() ,
, ![]() .
.
∵∠EDC=30°,
∴ ![]() .
.
∴FE=FC﹣EC=1.
【解析】(1)连接OD,根据等边三角形的性质求出∠ODE=90°,根据切线的判定定理证明即可;(2)连接AD,BF,根据等边三角形的性质求出DC、CF,根据直角三角形的性质求出EC,结合图形计算即可.


科目:初中数学 来源: 题型:
【题目】已知二次函数的解析式是y=x2﹣2x﹣3
(1)用配方法将y=x2﹣2x﹣3化成y=a(x﹣h)2+k的形式;
(2)在直角坐标系中,用五点法画出它的图像; 
(3)利用图象求当x为何值时,函数值y<0
(4)当x为何值时,y随x的增大而减小?
(5)当﹣3<x<3时,观察图象直接写出函数值y的取值的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发沿图中某一个扇形顺时针匀速运动,设∠APB=y(单位:度),如果y与点P运动的时间x(单位:秒)的函数关系的图象大致如图2所示,那么点P的运动路线可能为( )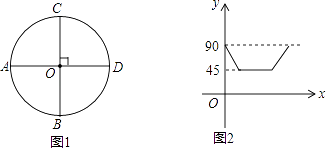
A.O→B→A→O
B.O→A→C→O
C.O→C→D→O
D.O→B→D→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”,“科技制作”,“数学思维”,“阅读写作”这四个选修项目的学生(每人限报一课)进行抽样调查,下面是根据收集的数据绘制的不完整的统计图:
请根据图中提供的信息,解答下面的问题:
(1)此次共调查了___名学生,扇形统计图中“艺术鉴赏”部分的圆心角是___度;
(2)此次调查“数学思维”的人数为_________,并补充完整条形图;
(3)现该校共有600名学生报名参加这四个选修项目,请你估计其中有____名学生选修“科技制作”项目.
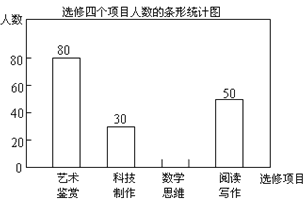
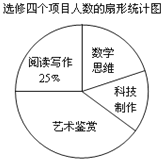
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为7,△FCB的周长为19,求FC的长.
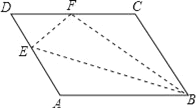
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1。在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换。若骰子的初始位置为图1所示的状态,那么按上述规则连续完成14次变换后,骰子朝上一面的点数是_____________________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近两年,国际市场黄金价格涨幅较大,中国交通银行推出“沃德金”的理财产品,即以黄金为投资产品,投资者从黄金价格的上涨中赚取利润.上周五黄金的收盘价为![]() 元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六、星期日休市)
元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六、星期日休市)
星期 | 一 | 二 | 三 | 四 | 五 |
收盘价的变化(与前一天收盘价比较) |
|
|
|
|
|
问
![]() 本周星期三黄金的收盘价是多少?
本周星期三黄金的收盘价是多少?
![]() 本周黄金收盘时的最高价、最低价分别是多少?
本周黄金收盘时的最高价、最低价分别是多少?
![]() 上周,小王以周五的收盘价
上周,小王以周五的收盘价![]() 元/克买入黄金
元/克买入黄金![]() 克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金
克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金![]() 克,他的收益情况如何?
克,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答问题.
饮水问题是关系到学生身心健康的重要生活环节,东坡中学共有教学班24个,平均每班有学生50人,经估算,学生一年在校时间约为240天(除去各种节假日),春、夏、秋、冬季各60天.原来,学生饮水一般都是购纯净水(其他碳酸饮料或果汁价格更高),纯净水零售价为1.5元/瓶,每个学生春、秋、冬季平均每天买1瓶纯净水,夏季平均每天要买2瓶纯净水,学校为了减轻学生消费负担,要求每个班自行购买1台冷热饮水机,经调查,购买一台功率为500 W的冷热饮水机约为150元,纯净水每桶6元,每班春、秋两季,平均每1.5天购买4桶,夏季平均每天购买5桶,冬季平均每天购买1桶,饮水机每天开10小时,当地民用电价为0.50元/度.
问题:
(1)在未购买饮水机之前,全年平均每个学生要花费多少钱来购买纯净水饮用?
(2)在购买饮水机解决学生饮水问题后,每班当年共要花费多少元?
(3)这项便利学生的措施实施后,东坡中学当年全体学生共节约多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=ax2﹣2(a﹣1)x+a﹣2(a>0).
(1)求证:抛物线与x轴有两个交点;
(2)设抛物线与x轴有两个交点的横坐标分别为x1 , x2 , (其中x1>x2).若y是关于a的函数,且y=ax2+x1 , 求这个函数的表达式;
(3)在(2)的条件下,结合函数的图象回答:若使y≤﹣3a2+1,则自变量a的取值范围为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com