
【题目】按下面的程序计算: 
当输入x=100时,输出结果是299;当输入x=50时,输出结果是466;如果输入x的值是正整数,输出结果是257,那么满足条件的x的值最多有( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:第一个数就是直接输出其结果的:3x﹣1=257, 解得:x=86,
第二个数是(3x﹣1)×3﹣1=257
解得:x=29;
第三个数是:3[3(3x﹣1)﹣1]﹣1=257,
解得:x=10,
第四个数是3{3[3(3x﹣1)﹣1]﹣1}﹣1=257,
解得:x= ![]() (不合题意舍去);
(不合题意舍去);
第五个数是3(81x﹣40)﹣1=257,
解得:x= ![]() (不合题意舍去);
(不合题意舍去);
故满足条件所有x的值是86、29或10共3个.
故选C.
【考点精析】关于本题考查的代数式求值,需要了解求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】我市去年有4.7万名考生参加了中考,为了解这些考生的数学成绩,从中抽取了4000名考生的数学成绩进行统计分析,以下说法正确的是( )
A. 这4000名考生是总体的一个样本
B. 这4.7万名考生的数学成绩是总体
C. 每位考生是个体
D. 抽取的4000名考生是样本容量
查看答案和解析>>
科目:初中数学 来源: 题型:
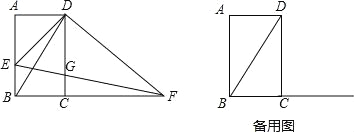
【题目】如图,在矩形ABCD中,BC=1,∠CBD=60°,点E是AB边上一动点(不与点A,B重合),连接DE,过点D作DF⊥DE交BC的延长线于点F,连接EF交CD于点G.
(1)求证:△ADE∽△CDF;
(2)求∠DEF的度数;
(3)设BE的长为x,△BEF的面积为y.
①求y关于x的函数关系式,并求出当x为何值时,y有最大值;
②当y为最大值时,连接BG,请判断此时四边形BGDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在6×6的方格纸中,给出如下三种变换:P变换,Q变换,R变换.将图形F沿x轴向右平移1格得到图形F1,称为作1次P变换;将图形F沿y轴翻折得到图形F2,称为作1次Q变换;将图形F绕坐标原点顺时针旋转90°得到图形F3,称为作1次R变换.规定:PQ变换表示先作1次Q变换,再作1次P变换;QP变换表示先作1次P变换,再作1次Q变换;Rn变换表示作n次R变换,解答下列问题:
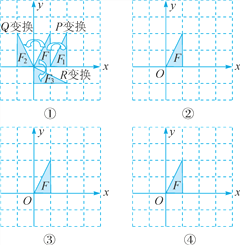
(1)作R4变换相当于至少作__ __次Q变换.
(2)请在图②中画出图形F作R2017变换后得到的图形F4.
(3)PQ变换与QP变换是否是相同的变换?请在图③中画出PQ变换后得到的图形F5,在图④中画出QP变换后得到的图形F6.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的 ![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该超市第二次以第一次的进价又购进甲、乙两种商品.其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售.第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙种商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
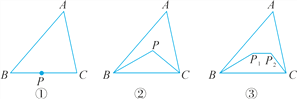
【题目】观察并探求下列各问题:
(1)如图①,在△ABC中,P为边BC上一点,则BP+PC__ __AB+AC(填“>”“<”或“=”).
(2)将(1)中的点P移到△ABC内,得图②,试观察比较△BPC的周长与△ABC的周长的大小,并说明理由.
(3)将(2)中的点P变为两个点P1,P2,得图③,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com