
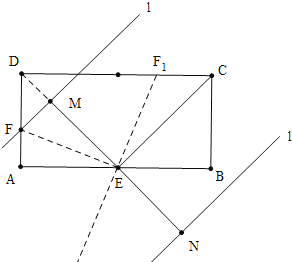
【题目】如图矩形,AB=2BC=4,E是AB二等分点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,沿直线EF折叠矩形ABCD,使点A落在直线l上,则DF=_____.

【答案】2![]() 或4﹣2
或4﹣2![]()
【解析】
分两种情况求解:直线l在直线CE上方时,连接DE证得△ADE、△ECB是等腰直角三角形,由此证得点A、点M关于直线EF对称,利用已知数据求得DF;直线l在直线EC下方时,利用对顶角相等得到∠DEF1=∠BEF1=∠DF1E,求出DF1=DE=2![]() .
.
如图,当直线l在直线CE上方时,连接DE交直线l于M,
∵AB=2BC=4,E是AB二等分点,
∴BC=2,BE=2=AE
∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC,
∵AB=4,AD=BC=2,
∴AD=AE=EB=BC=2,
∴△ADE、△ECB是等腰直角三角形,
∴∠AED=∠BEC=45°,
∴∠DEC=90°,
∵l∥EC,
∴ED⊥l,
∴EM=2=AE,
∴点A、点M关于直线EF对称,
∵∠MDF=∠MFD=45°,
∴DM=MF=DE﹣EM=2![]() ﹣2,
﹣2,
∴DF=![]() DM=4﹣2
DM=4﹣2![]() ,
,
当直线l在直线EC下方时,
∵∠DEF1=∠BEF1=∠DF1E,
∴DF1=DE=2![]() ,
,
综上所述DF的长为2![]() 或4﹣2
或4﹣2![]() .
.
故答案为2![]() 或4﹣2
或4﹣2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】国家近年来实施了新一轮农村电网改造升级工程,解决了农村供电“最后1公里”问题,电力公司在改造时把某一输电线铁塔建在了一个坡度为1:0.75的山坡CD的平台BC上(如图),测得∠AED=52°,BC=5米,CD=35米,DE=19米,则铁塔AB的高度约为(参考数据:sin52°≈0.79,tan52°≈1.28)( )

A.28米B.29.6米C.36.6米D.57.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在直角坐标系中△ABC的顶点A、B、C三点坐标为A(7,1),B(8,2),C(9,0).
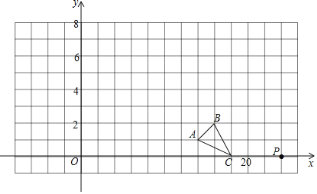
(1)请在图中画出△ABC的一个以点P(12,0)为位似中心,相似比为3的位似图形△A'B'C'(要求与△ABC在P点同一侧);
(2)直接写出A'点的坐标;
(3)直接写出△A'B'C'的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
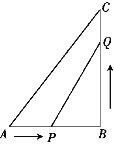
【题目】如图,在△ABC中,∠B=90°,AB=5 cm,BC=7 cm,点P从点A开始沿AB边向点B以1 cm/s的速度移动,同时点Q从点B开始沿BC向点C以2cm/s的速度移动.当一个点到达终点时另一点也随之停止运动,运动时间为x秒(x>0).
(1)求几秒后,PQ的长度等于5 cm.
(2)运动过程中,△PQB的面积能否等于8 cm2?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).
(1)求这个二次函数的表达式;
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,A(﹣4,0).正方形OBCD的顶点B在x轴的负半轴上,点C在第二象限.现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG.
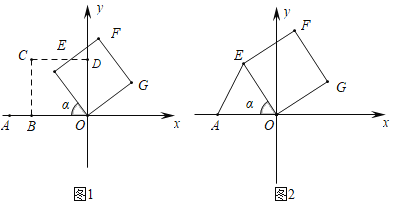
(1)如图2,若α=60°,OE=OA,求直线EF的函数表达式.
(2)若α为锐角,tanα=![]() ,当AE取得最小值时,求正方形OEFG的面积.
,当AE取得最小值时,求正方形OEFG的面积.
(3)当正方形OEFG的顶点F落在y轴上时,直线AE与直线FG相交于点P,△OEP的其中两边之比能否为![]() :1?若能,求点P的坐标;若不能,试说明理由.
:1?若能,求点P的坐标;若不能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化。类似的,可以在等腰三角形中建立边角之间的联系。我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can).
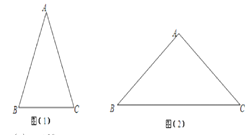
如图(1)在△![]() 中,
中,![]() ,底角
,底角![]() 的邻对记作
的邻对记作![]() ,这时
,这时![]() ,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义解下列问题:
,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义解下列问题:
(1)![]() = ;
= ;
(2)如图(2),在△![]() 中,
中,![]() ,
,![]() ,
,![]() ,求△
,求△![]() 的周长
的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
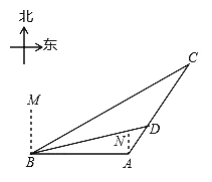
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外如图,某天我国一艘海监船巡航到![]() 港口正西方的
港口正西方的![]() 处时,发现在
处时,发现在![]() 的北偏东
的北偏东![]() 方向,相距
方向,相距![]() 海里处的
海里处的![]() 点有一可疑船只正沿
点有一可疑船只正沿![]() 方向行驶,
方向行驶,![]() 点在
点在![]() 港口的北偏东
港口的北偏东![]() 方向上,海监船向
方向上,海监船向![]() 港口发出指令,执法船立即从
港口发出指令,执法船立即从![]() 港口沿
港口沿![]() 方向驶出,在
方向驶出,在![]() 处成功拦截可疑船只,此时
处成功拦截可疑船只,此时![]() 点与
点与![]() 点的距离为
点的距离为![]() 海里.
海里.
(1)求![]() 的度数与
的度数与![]() 点到直线
点到直线![]() 的距离;
的距离;
(2)执法船从![]() 到
到![]() 航行了多少海里?(结果保留根号)
航行了多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)试探究t为何值时,△BPQ的面积是![]() cm2;
cm2;
(3)直接写出t为何值时,△BPQ是等腰三角形;
(4)连接AQ,CP,若AQ⊥CP,直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com