
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)试探究t为何值时,△BPQ的面积是![]() cm2;
cm2;
(3)直接写出t为何值时,△BPQ是等腰三角形;
(4)连接AQ,CP,若AQ⊥CP,直接写出t的值.
【答案】(1)t=1,t=![]() ;(2)t1=
;(2)t1=![]() 或t2=
或t2=![]() ;(3) 当t=
;(3) 当t=![]() 或
或![]() 或
或![]() 时,△BPQ是等腰三角形;(4)t=
时,△BPQ是等腰三角形;(4)t=![]()
【解析】
(1)由勾股定理可求AB的长,分两种情况讨论,由相似三角形的性质可求解;
(2)过点P作PE⊥BC于E,由平行线分线段成比例可得PE=3t,由三角形的面积公式列出方程可求解;
(3)分三种情况讨论,由等腰三角形的性质可求解;
(4)过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,MC=8-4t,根据△ACQ∽△CMP,得出AC:CM=CQ:MP,代入计算即可.
(1)∵∠ACB=90°,AC=6cm,BC=8cm,
∴AB=![]() =
=![]() =10cm,
=10cm,
∵△BPQ与△ABC相似,且∠B=∠B,
∴![]() 或
或![]() ,
,
当![]() 时,
时,
∴![]() ,
,
∴t=1,
当![]() ,
,
∴![]() ,
,
∴t=![]() ;
;
(2)如图1,过点P作PE⊥BC于E,

∴PE∥AC,
∴![]() ,
,
∴PE=![]() =3t,.
=3t,.
∴S△BPQ=![]() ×(8﹣4t)×3t=
×(8﹣4t)×3t=![]() ,
,
∴t1=![]() 或t2=
或t2=![]() ;
;
(3)①当PB=PQ时,如图1,过P作PE⊥BQ,
则BE=![]() BQ=4﹣2t,PB=5t,
BQ=4﹣2t,PB=5t,
由(2)可知PE=3t,
∴BE=![]() =
=![]() =4t,
=4t,
∴4t=4﹣2t,
∴t=![]()
②当PB=BQ时,即5t=8﹣4t,
解得:t=![]() ,
,
③当BQ=PQ时,如图2,过Q作QG⊥AB于G,

则BG=![]() PB=
PB=![]() t,BQ=8﹣4t,
t,BQ=8﹣4t,
∵△BGQ∽△ACB,
∴![]() ,
,
∴
解得:t=![]() .
.
综上所述:当t=![]() 或
或![]() 或
或![]() 时,△BPQ是等腰三角形;
时,△BPQ是等腰三角形;
(4)过P作PM⊥BC于点M,AQ,CP交于点N,如图3所示:则PB=5t,

∵AC⊥BC
∴△PMB∽△ACB,
∴![]() =
=![]()
∴BM=4t,PM=3t,且BQ=8﹣4t,BC=8,
∴MC=8﹣4t,CQ=4t,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
∵∠ACQ=∠PMC,
∴△ACQ∽△CMP,
∴![]() ,
,
∴![]()
∴t=![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
(1)求证:AB=CE;
(2)若![]() ,则四边形ABEC是什么特殊四边形?请说明理由.
,则四边形ABEC是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
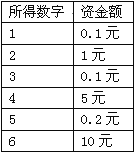
【题目】有时我们可以看到这样的转盘游戏:如图所示,你只要出1元钱就可以随意地转动转盘,转盘停止时指针落在哪个区域,你就按照这个区域所示的数字相应地顺时针跳过几格,然后按照下图所示的说明确定你的资金是多少.例如,当指针指向 “2”区域时候,你就向前跳过两个格到“5”,按奖金说明,“5”所示的资金为0.2元,你就可以得0.2元.请问这个游戏公平吗?能否用你所学的知识揭示其中的秘密?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
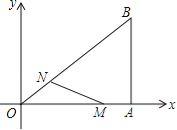
(1)求点N的坐标(用含x的代数式表示);
(2)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
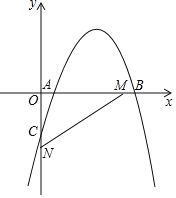
【题目】如图,平面直角坐标系中,抛物线y=﹣x2+4x+m﹣4(m为常数)与y轴的交点为C,M(3,0)与N(0,﹣2)分别是x轴、y轴上的点
(1)当m=1时,求抛物线顶点坐标.
(2)若3≤x≤3+m时,函数y=﹣x2+4x+m﹣4有最小值﹣7,求m的值.
(3)若抛物线与线段MN有公共点,直接写出m的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
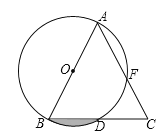
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
(1)AB与AC的大小有什么关系?请说明理由;
(2)若AB=8,∠BAC=45°,求:图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题12分)如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.

(1)求证:CD为⊙O的切线;
(2)求证:∠C=2∠DBE.
(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com