
ЁОЬтФПЁПЃЈ12ЗжЃЉШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌRtЁїOABЕФжБНЧЖЅЕуAдкxжсЩЯЃЌOA=4ЃЌAB=3ЃЎЖЏЕуMДгЕуAГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЃЌбиAOЯђжеЕуOвЦЖЏЃЛЭЌЪБЕуNДгЕуOГіЗЂЃЌвдУПУы1ЃЎ25ИіЕЅЮЛГЄЖШЕФЫйЖШЃЌбиOBЯђжеЕуBвЦЖЏЃЎЕБСНИіЖЏЕудЫЖЏСЫxУыЃЈ0ЃМxЃМ4ЃЉЪБЃЌНтД№ЯТСаЮЪЬтЃК
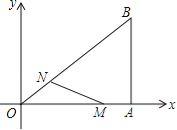
ЃЈ1ЃЉЧѓЕуNЕФзјБъЃЈгУКЌxЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉЩшЁїOMNЕФУцЛ§ЪЧSЃЌЧѓSгыxжЎМфЕФКЏЪ§БэДяЪНЃЛЕБxЮЊКЮжЕЪБЃЌSгазюДѓжЕЃПзюДѓжЕЪЧЖрЩйЃП
ЃЈ3ЃЉдкСНИіЖЏЕудЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкФГвЛЪБПЬЃЌЪЙЁїOMNЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіxЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈxЃЌ ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ2ЃЉЕБx=2ЪБЃЌSгазюДѓжЕЃЌзюДѓжЕЪЧ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉxЕФжЕЪЧ2УыЛђ![]() УыЃЎ
УыЃЎ
ЁОНтЮіЁПЪдЬтЃЈ1ЃЉгЩЙДЙЩЖЈРэЧѓГіOBЃЌзїNPЁЭOAгкPЃЌдђNPЁЮABЃЌЕУГіЁїOPNЁзЁїOABЃЌЕУГіБШР§ЪН![]() ЃЌЧѓГіOPЁЂPNЃЌМДПЩЕУГіЕуNЕФзјБъЃЛ
ЃЌЧѓГіOPЁЂPNЃЌМДПЩЕУГіЕуNЕФзјБъЃЛ
ЃЈ2ЃЉгЩШ§НЧаЮЕФУцЛ§ЙЋЪНЕУГіSЪЧxЕФЖўДЮКЏЪ§ЃЌМДПЩЕУГіSЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЃКЂйШєЁЯOMN=90ЁуЃЌдђMNЁЮABЃЌгЩЦНааЯпЕУГіЁїOMNЁзЁїOABЃЌЕУГіБШР§ЪНЃЌМДПЩЧѓГіxЕФжЕЃЛ
ЂкШєЁЯONM=90ЁуЃЌдђЁЯONM=ЁЯOABЃЌжЄГіЁїOMNЁзЁїOBAЃЌЕУГіБШР§ЪНЃЌЧѓГіxЕФжЕМДПЩЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉИљОнЬтвтЕУЃКMA=xЃЌON=1ЃЎ25xЃЌ
дкRtЁїOABжаЃЌгЩЙДЙЩЖЈРэЕУЃКOB=![]() =5ЃЌ
=5ЃЌ
зїNPЁЭOAгкPЃЌШчЭМ1ЫљЪОЃК
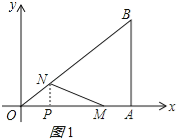
дђNPЁЮABЃЌ
ЁрЁїOPNЁзЁїOABЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУЃКOP=xЃЌPN= ![]() ЃЌ
ЃЌ
ЁрЕуNЕФзјБъЪЧЃЈxЃЌ ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ2ЃЉдкЁїOMNжаЃЌOM=4ЉxЃЌOMБпЩЯЕФИпPN= ![]() ЃЌ
ЃЌ
ЁрS=![]() OMPN=
OMPN=![]() ЃЈ4ЉxЃЉ
ЃЈ4ЉxЃЉ ![]() =Љ
=Љ![]()
![]() +
+![]() xЃЌ
xЃЌ
ЁрSгыxжЎМфЕФКЏЪ§БэДяЪНЮЊS=Љ![]()
![]() +
+![]() xЃЈ0ЃМxЃМ4ЃЉЃЌ
xЃЈ0ЃМxЃМ4ЃЉЃЌ
ХфЗНЕУЃКS=Љ![]()
![]() +
+![]() ЃЌ
ЃЌ
ЁпЉ![]() ЃМ0ЃЌ
ЃМ0ЃЌ
ЁрSгазюДѓжЕЃЌ
ЕБx=2ЪБЃЌSгазюДѓжЕЃЌзюДѓжЕЪЧ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉДцдкФГвЛЪБПЬЃЌЪЙЁїOMNЪЧжБНЧШ§НЧаЮЃЌРэгЩШчЯТЃК
ЗжСНжжЧщПіЃКЂйШєЁЯOMN=90ЁуЃЌШчЭМ2ЫљЪОЃК
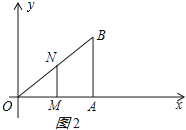
дђMNЁЮABЃЌ
ДЫЪБOM=4ЉxЃЌON=1ЃЎ25xЃЌ
ЁпMNЁЮABЃЌ
ЁрЁїOMNЁзЁїOABЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУЃКx=2ЃЛ
ЂкШєЁЯONM=90ЁуЃЌШчЭМ3ЫљЪОЃК
дђЁЯONM=ЁЯOABЃЌ
ДЫЪБOM=4ЉxЃЌON=1ЃЎ25xЃЌ
ЁпЁЯONM=ЁЯOABЃЌЁЯMON=ЁЯBOAЃЌ
ЁрЁїOMNЁзЁїOBAЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУЃКx=![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃКxЕФжЕЪЧ2УыЛђ![]() УыЃЎ
УыЃЎ



 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуAЃЌBЮЊЖЈЕуЃЌЖЈжБЯпl//ABЃЌPЪЧlЩЯвЛЖЏЕуЃЎЕуMЃЌNЗжБ№ЮЊPAЃЌPBЕФжаЕуЃЌЖдгкЯТСаИїжЕЃКЂйЯпЖЮMNЕФГЄЃЛЂкЁїPMNЕФУцЛ§ЃЛЂлЁїPABЕФжмГЄЃЛЂмЁЯAPBЕФДѓаЁЃЛЂнжБЯпMNЃЌABжЎМфЕФОрРыЃЎЦфжаЛсЫцЕуPЕФвЦЖЏЖјВЛИФБфЕФЪЧЃЈ ЃЉ

A. ЂйЂкЂл B. ЂйЂкЂн C. ЂкЂлЂм D. ЂкЂмЂн
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
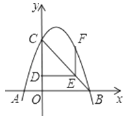
ЁОЬтФПЁПШчЭМЫљЪОЃЌХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉОЙ§AЃЈЉ1ЃЌ0ЃЉЁЂBЃЈ3ЃЌ0ЃЉЁЂCЃЈ0ЃЌ3ЃЉШ§ЕуЃЎЕуDДгCГіЗЂЃЌбиЯпЖЮCOвд1ИіЕЅЮЛ/УыЕФЫйЖШЯђжеЕуOдЫЖЏЃЌЙ§ЕуDзїOCЕФДЙЯпНЛBCгкЕуEЃЌзїEFЁЮOCЃЌНЛХзЮяЯпгкЕуFЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉаЁУїдкЬНОПЕуDдЫЖЏЪБЗЂЯжЃЌЂйЕБЕуDгыЕуCжиКЯЪБЃЌEFГЄЖШПЩПДзїOЃЛЂкЕБЕуDгыЕуOжиКЯЪБЃЌEFГЄЖШвВПЩвдПДзїOЃЌгкЪЧЫћВТЯыЃКЩшЕуDдЫЖЏЕНOCжаЕуЮЛжУЪБЃЌЕБЯпЖЮEFзюГЄЃЌФуШЯЮЊЫћВТЯыЪЧЗёе§ШЗЃЌЮЊЪВУДЃП
ЃЈ3ЃЉСЌНгCFЁЂDFЃЌЧыжБНгаДГіЁїCDFЮЊЕШбќШ§НЧаЮЪБЫљгаtЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
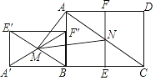
ЁОЬтФПЁПШчЭМЃЌвбжЊОиаЮABCDТњзуABЃКBC=1ЃК ![]() ЃЌАбОиаЮABCDЖделЃЌЪЙCDгыABжиКЯЃЌЕУелКлEFЃЌАбОиаЮABFEШЦЕуBФцЪБеыа§зЊ90ЁуЃЌЕУЕНОиаЮAЁфBFЁфEЁфЃЌСЌНсEЁфBЃЌНЛAЁфFЁфгкЕуMЃЌСЌНсACЃЌНЛEFгкЕуNЃЌСЌНсAMЃЌMNЃЌШєОиаЮABCDУцЛ§ЮЊ8ЃЌдђЁїAMNЕФУцЛ§ЮЊЃЈ ЃЉ
ЃЌАбОиаЮABCDЖделЃЌЪЙCDгыABжиКЯЃЌЕУелКлEFЃЌАбОиаЮABFEШЦЕуBФцЪБеыа§зЊ90ЁуЃЌЕУЕНОиаЮAЁфBFЁфEЁфЃЌСЌНсEЁфBЃЌНЛAЁфFЁфгкЕуMЃЌСЌНсACЃЌНЛEFгкЕуNЃЌСЌНсAMЃЌMNЃЌШєОиаЮABCDУцЛ§ЮЊ8ЃЌдђЁїAMNЕФУцЛ§ЮЊЃЈ ЃЉ
A. 4 ![]() B. 4 C. 2 D. 1
B. 4 C. 2 D. 1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌCDЪЧABБпЩЯЕФжаЯпЃЌEЪЧCDЕФжаЕуЃЌЙ§ЕуCзїABЕФЦНааЯпНЛAEЕФбгГЄЯпгкЕуFЃЌСЌНгBFЃЎ
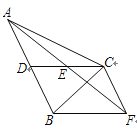
(1) ЧѓжЄЃКCFЃНADЃЛ
(2) ШєCAЃНCBЃЌЁЯACBЃН90ЁуЃЌЪдХаЖЯЫФБпаЮCDBFЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАДвЊЧѓЭъГЩЯТСаИїаЁЬтЃЎ
ЃЈ1ЃЉНтЗНГЬЃКx2+6x+2=2x+7ЃЛ
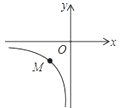
ЃЈ2ЃЉШчЭМЪЧЗДБШР§КЏЪ§y=![]() дкЕкШ§ЯѓЯоЕФЭМАИЃЌЕуMдкИУЭМЯѓЩЯЃЌЧвЕуMЕНЕуxжсЃЌyжсЕФОрРыЖМЕШгк|k|ЃЌЧѓkЕФжЕЃЎ
дкЕкШ§ЯѓЯоЕФЭМАИЃЌЕуMдкИУЭМЯѓЩЯЃЌЧвЕуMЕНЕуxжсЃЌyжсЕФОрРыЖМЕШгк|k|ЃЌЧѓkЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЗДБШР§КЏЪ§![]() ЃЈkЮЊГЃЪ§ЃЌkЁй1ЃЉЃЎ
ЃЈkЮЊГЃЪ§ЃЌkЁй1ЃЉЃЎ
ЃЈЂёЃЉЦфЭМЯѓгые§БШР§КЏЪ§y=xЕФЭМЯѓЕФвЛИіНЛЕуЮЊPЃЌШєЕуPЕФзнзјБъЪЧ2ЃЌЧѓkЕФжЕЃЛ
ЃЈЂђЃЉШєдкЦфЭМЯѓЕФУПвЛжЇЩЯЃЌyЫцxЕФдіДѓЖјМѕаЁЃЌЧѓkЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂѓЃЉШєЦфЭМЯѓЕФвЛжЇЮЛгкЕкЖўЯѓЯоЃЌдкетвЛжЇЩЯШЮШЁСНЕуAЃЈx1ЃЌy1ЃЉЁЂBЃЈx2ЃЌy2ЃЉЃЌЕБy1ЃОy2ЪБЃЌЪдБШНЯx1гыx2ЕФДѓаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЗДБШР§КЏЪ§![]() ЃЈkЮЊГЃЪ§ЃЌkЁй0ЃЉЕФЭМЯѓОЙ§ЕуAЃЈ2ЃЌ3ЃЉЃЎ
ЃЈkЮЊГЃЪ§ЃЌkЁй0ЃЉЕФЭМЯѓОЙ§ЕуAЃЈ2ЃЌ3ЃЉЃЎ
ЃЈ1ЃЉЧѓетИіКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉХаЖЯЕуBЃЈЃ1ЃЌ6ЃЉЃЌCЃЈ3ЃЌ2ЃЉЪЧЗёдкетИіКЏЪ§ЕФЭМЯѓЩЯЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБЃ3ЃМxЃМЃ1ЪБЃЌЧѓyЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
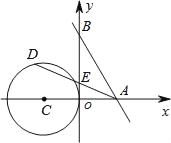
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпy=-![]() x+2
x+2![]() гыСНзјБъжсЗжБ№НЛгкAЁЂBСНЕуЃЌЁбCЕФдВаФзјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЌАыОЖЮЊ2ЃЌШєDЪЧЁбCЩЯЕФвЛИіЖЏЕуЃЌЯпЖЮDAгыyжсНЛгкЕуEЃЌдђЁїABEУцЛ§SЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
гыСНзјБъжсЗжБ№НЛгкAЁЂBСНЕуЃЌЁбCЕФдВаФзјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЌАыОЖЮЊ2ЃЌШєDЪЧЁбCЩЯЕФвЛИіЖЏЕуЃЌЯпЖЮDAгыyжсНЛгкЕуEЃЌдђЁїABEУцЛ§SЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com