
【题目】如图,在△ABC中,∠B=90°,AB=5 cm,BC=7 cm,点P从点A开始沿AB边向点B以1 cm/s的速度移动,同时点Q从点B开始沿BC向点C以2cm/s的速度移动.当一个点到达终点时另一点也随之停止运动,运动时间为x秒(x>0).
(1)求几秒后,PQ的长度等于5 cm.
(2)运动过程中,△PQB的面积能否等于8 cm2?并说明理由.
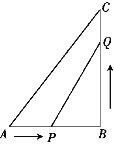
【答案】(1)2秒后PQ的长度等于5 cm;(2)△PQB的面积不能等于8 cm2.
【解析】
(1)根据PQ=5,利用勾股定理BP2+BQ2=PQ2,求出即可;
(2)通过判定得到的方程的根的判别式即可判定能否达到8cm2.
解:(1)根据题意,得BP=(5-x),BQ=2x.
当PQ=5时,在Rt△PBQ中,BP2+BQ2=PQ2,
∴(5-x)2+(2x)2=52,
5x2-10x=0,
5x(x-2)=0,
x1=0(舍去),x2=2,
答:2秒后PQ的长度等于5 cm.
(2)设经过x秒以后,△PBQ面积为8,
![]() ×(5-x)×2x=8.
×(5-x)×2x=8.
整理得x2-5x+8=0,
Δ=25-32=-7<0,
∴△PQB的面积不能等于8 cm2.


科目:初中数学 来源: 题型:
【题目】石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______ 件,每件盈利______ 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,动点P以
,动点P以![]() 的速度从A点出发,沿
的速度从A点出发,沿![]() 向C点移动,同时动点Q以
向C点移动,同时动点Q以![]() 的速度从点C出发,沿
的速度从点C出发,沿![]() 向点B移动,设P、Q两点移动的时间为t秒
向点B移动,设P、Q两点移动的时间为t秒![]() .
.
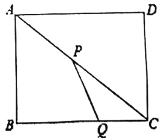
(1)t为多少时,以P、Q、C为顶点的三角形与![]() 相似?
相似?
(2)在P、Q两点移动过程中,四边形![]() 与
与![]() 的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
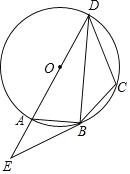
(1)求证:DB平分∠ADC;
(2)若EB=10,CD=9,tan∠ABE=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学在一次数学测验中解答的填空题,其中答对的是( )
A.若![]() ,则x=2B.若
,则x=2B.若![]() 的一个根是1,则k=2
的一个根是1,则k=2
C.若![]() ,则x=2D.若
,则x=2D.若![]() 的值为0,则x=1或2
的值为0,则x=1或2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() ,
,![]() (
(![]() )同时与
)同时与![]() 交于一点
交于一点![]() 时,点
时,点![]() ,
,![]() 和点
和点![]() 构成
构成![]() ,在此过程中,
,在此过程中,![]() 周长的最小值是__________.
周长的最小值是__________.
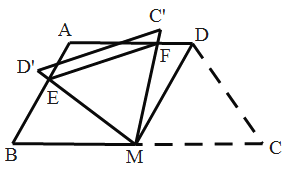
查看答案和解析>>
科目:初中数学 来源: 题型:
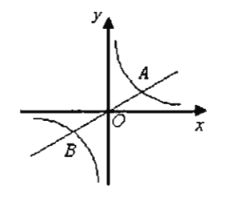
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() (
(![]() )交于
)交于![]() ,
,![]() 两点,且点
两点,且点![]() 的横坐标为6.
的横坐标为6.
(1)求![]() 的值;
的值;
(2)若双曲线![]() (
(![]() )上一点
)上一点![]() 的纵坐标为9,求
的纵坐标为9,求![]() 的面积;
的面积;
(3)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() (
(![]() )于
)于![]() ,
,![]() 两点(
两点(![]() 点在第一象限),若由点
点在第一象限),若由点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点组成的四边形面积为96,求点
为顶点组成的四边形面积为96,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
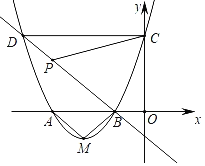
【题目】如图,抛物线y=(x+2)2+m与x轴交于A,B两点,与y轴交于点C.点D在抛物线上,且与点C关于抛物线的对称轴对称,抛物线的顶点为M,点B的坐标为(﹣1,0).
(1)求抛物线的解析式及A,C,D的坐标;
(2)判断△ABM的形状,并证明你的结论;
(3)若点P是直线BD上一个动点,是否存在以P,C,D为顶点的三角形与△ABD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com