
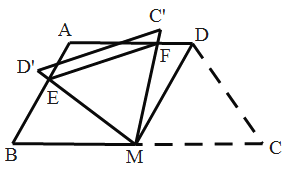
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() ,
,![]() (
(![]() )同时与
)同时与![]() 交于一点
交于一点![]() 时,点
时,点![]() ,
,![]() 和点
和点![]() 构成
构成![]() ,在此过程中,
,在此过程中,![]() 周长的最小值是__________.
周长的最小值是__________.
【答案】![]()
【解析】
连接AM,过点D作DN⊥CM于N,AQ⊥BM于Q,首先易证四边形AQND是平行四边形,四边形ABCD是等腰梯形,然后根据含30度直角三角形的性质可得CN=2,BQ=2,求出CM=CD,证明△CMD、△ABM、△AMD是等边三角形,然后可得∠BME=∠AMF,利用ASA证明△BME≌△AMF,求出BE=AF,即可得到AE+AF=AE+BE=AB=4,故当ME最短时,![]() 的周长最小,此时ME⊥AB,根据等边三角形的性质和勾股定理求出ME即可.
的周长最小,此时ME⊥AB,根据等边三角形的性质和勾股定理求出ME即可.
解:如图,连接AM,过点D作DN⊥CM于N,AQ⊥BM于Q,
∴AQ∥DN,
∵AD∥BC,![]() ,
,
∴四边形AQND是平行四边形,四边形ABCD是等腰梯形,
∴QN=AD=4,![]() ,
,
∴CN=![]() ,BQ=
,BQ=![]() ,
,
∴BC=BQ+QN+CN=2+4+2=8,即BC=2CD,
∵![]() 是
是![]() 的中点,
的中点,
∴CM=CD,
∴△CMD是等边三角形,
同理可得△ABM是等边三角形,
∴△AMD是等边三角形,
∴∠BMA=∠DMC=∠EMF=60°,
∴∠BME=∠AMF,
在△BME和△AMF中,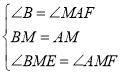 ,
,
∴△BME≌△AMF(ASA),
∴BE=AF,
∴AE+AF=AE+BE=AB=4,
∴当ME最短时,![]() 的周长最小,
的周长最小,
即ME⊥AB时,![]() 的周长最小,
的周长最小,
∵△ABM是等边三角形,BM=AM=4,
∴ME⊥AB时,BE=2,
∴![]() ,
,
∴△AEF的周长最小值为![]() ,
,
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】阅读材料,回答下列问题:
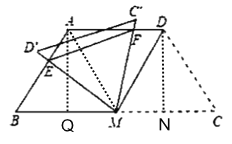
阿尔花拉子米(约780~约850),著名阿拉伯数学家、天文学家、地理学家,是代数与算术的整理者,被誉为“代数之父”.他利用正方形图形巧妙解出了一元二次方程x2+2x﹣35=0的一个解.
将边长为x的正方形和边长为1的正方形,外加两个长方形,长为x,宽为1,拼合在一起面积就是x2+2×1+1×1,即x2+2x+1,而由原方程x2+2x﹣35=0变形得x2+2x+1=35+1,即右边边长为x+1的正方形面积为36.所以(x+1)2=36,则x=5.
(1)上述求解过程中所用的方法与下列哪种方法是一致的 .
A.直接开平方法 B.公式法
C.配方法 D.因式分解法
(2)所用的数学思想方法是 .
A.分类讨论思想 B.数形结合思想 C.转化思想
(3)运用上述方法构造出符合方程x2+4x﹣5=0的一个正根的正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
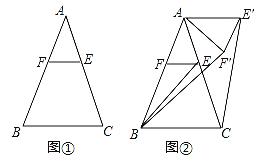
【题目】已知,△ABC中,AB=AC,点E是边AC上一点,过点E作EF∥BC交AB于点F
(1)如图①,求证:AE=AF;
(2)如图②,将△AEF绕点A逆时针旋转α(0°<α<144°)得到△AE′F′.连接CE′BF′.
①若BF′=6,求CE′的长;
②若∠EBC=∠BAC=36°,在图②的旋转过程中,当CE′∥AB时,直接写出旋转角α的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
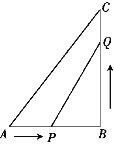
【题目】如图,在△ABC中,∠B=90°,AB=5 cm,BC=7 cm,点P从点A开始沿AB边向点B以1 cm/s的速度移动,同时点Q从点B开始沿BC向点C以2cm/s的速度移动.当一个点到达终点时另一点也随之停止运动,运动时间为x秒(x>0).
(1)求几秒后,PQ的长度等于5 cm.
(2)运动过程中,△PQB的面积能否等于8 cm2?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
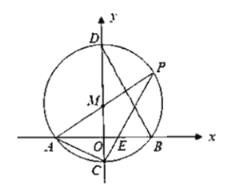
【题目】如图,在平面直角坐标系中,以点![]() 为圆心,作
为圆心,作![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于
轴于![]() 、
、![]() 两点,连结
两点,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,连结
,连结![]() 交
交![]() 轴于点
轴于点![]() ,连结
,连结![]() ,
,![]() .
.
(1)求弦![]() 的长;
的长;
(2)求直线![]() 的函数解析式;
的函数解析式;
(3)连结![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
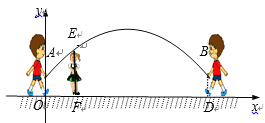
【题目】跳绳时,绳甩到最高处时的形状是抛物线. 正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0. 9米,身高为1. 4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E. 以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为![]() .
.
(1)求该抛物线的解析式;
(2)如果身高为1. 85米的小华也想参加跳绳,问绳子能否顺利从他头顶越过?请说明理由;
(3)如果一群身高在1. 4米到1. 7米之间的人站在OD之间,且离点O的距离为t米, 绳子甩到最高处时必须超过他们的头顶,请结合图像,写出t的取值范围_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
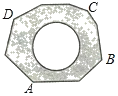
【题目】如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为2米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
掷小石子落在不规则图形内的总次数 | 50 | 150 | 300 | … |
小石子落在圆内(含圆上)的次数m | 20 | 59 | 123 | … |
小石子落在圆外的阴影部分(含外缘)的次数n | 29 | 91 | 176 | … |
(1)当投掷的次数很大时,则m:n的值越来越接近 (结果精确到0.1)
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在 附近(结果精确到0.1);
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是多少平方米?(结果保留π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com