
【题目】如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC. 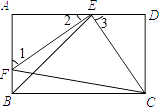
(1)求证:AE=DC;
(2)已知DC= ![]() ,求BE的长.
,求BE的长.
【答案】
(1)证明:在矩形ABCD中,∠A=∠D=90°,
∴∠1+∠2=90°,
∵EF⊥EC,
∴∠FEC=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
在△AEF和△DCE中,
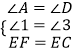 ,
,
∴△AEF≌△DCE(AAS),
∴AE=DC
(2)解:由(1)得AE=DC,
∴AE=DC= ![]() ,
,
在矩形ABCD中,AB=CD= ![]() ,
,
在R△ABE中,AB2+AE2=BE2,即( ![]() )2+(
)2+( ![]() )2=BE2,
)2=BE2,
∴BE=2
【解析】(1)根据矩形的性质和已知条件可证明△AEF≌△DCE,可证得AE=DC;(2)由(1)可知AE=DC,在Rt△ABE中由勾股定理可求得BE的长.
【考点精析】根据题目的已知条件,利用勾股定理的概念和矩形的性质的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等.


科目:初中数学 来源: 题型:
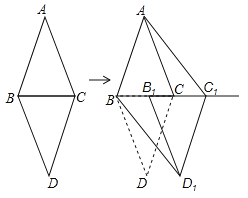
【题目】如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3cm.BC=2cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查的是( )
A. 对常州市居民日平均用水量的调查
B. 对一批LED节能灯使用寿命的调查
C. 对常州新闻频道“政风热线”栏目收视率的调查
D. 对某校八年级(2)班同学的视力情况的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (k>0).
(k>0).
(1)当k=![]() 时,求这个二次函数的顶点坐标;
时,求这个二次函数的顶点坐标;
(2)求证:关于x的一元次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
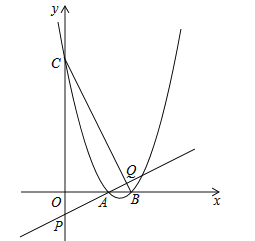
(3)如图,该二次函数与x轴交于A、B两点(A点在B点的左侧),与y轴交于C点,P是y轴负半轴上一点,且OP=1,直线AP交BC于点Q,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
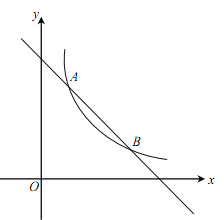
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中: 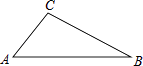
(1)用直尺和圆规,在AB上找一点D,使点D到B、C两点的距离相等(不写作法.保留作图痕迹)
(2)连接CD,已知CD=AC,∠B=25°,求∠ACB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com