
【题目】如图,∠AOB=∠COD=90°,OE平分∠AOC,∠AOD=120°.
(1)求∠BOC的度数;
(2)求∠BOE的度数.
【答案】
(1)解:∵∠AOB=∠COD=90°,∠AOD=120°,
∴∠BOC=360°﹣∠AOB﹣∠COD﹣∠AOD,
=360°﹣90°﹣90°﹣120°,
=60°.
(2)解:∵∠AOB=90°,∠BOC=60°,
∴∠AOC=∠AOB+∠BOC=90°+60°=150°,
又∵OE平分∠AOC,
∴∠COE= ![]() AOC=
AOC= ![]() ×150°=75°,
×150°=75°,
∴∠BOE=∠COE﹣∠BOC=75°﹣60°=15°.
【解析】(1)由周角定义结合已知条件得∠BOC=360°﹣∠AOB﹣∠COD﹣∠AOD即可得出答案.
(2)由已知条件得∠AOC=∠AOB+∠BOC=150°,再根据角平分线定义得∠COE= ![]() AOC=75°,由∠BOE=∠COE﹣∠BOC即可得出答案.
AOC=75°,由∠BOE=∠COE﹣∠BOC即可得出答案.


科目:初中数学 来源: 题型:
【题目】某工厂一种产品2013年的产量是100万件,计划2015年产量达到121万件,假设2013年到2015年这种产品产量的年增长率相同,求2013年到2015年这种产品产量的年增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学小组的同学为了解“阅读经典”活动的开展情况,随机调查了50名同学,对他们一周的阅读时间进行了统计,并绘制成如图所示的条形统计图,这组数据的中位数和众数分别是( )
A.中位数和众数都是8小时
B.中位数是25人,众数是20人
C.中位数是13人,众数是20人
D.中位数是6小时,众数是8小时
查看答案和解析>>
科目:初中数学 来源: 题型:
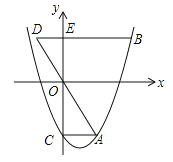
【题目】如图,抛物线![]() (m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
①斜边和一直角边对应相等的两个直角三角形全等;②有两边和它们的夹角对应相等的两个直角全角形全等;③一锐角和斜边对应相等的两个直角三角形全等;④两个锐角对应相等的两个直角三角形全等.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是( ) 
A.15°
B.20°
C.25°
D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com