
某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不能超过10000元,且生产B产品要超过38件,问有哪几种符合条件的生产方案?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,才能使生产这批产品的成本最低?请直接写出方案.
【考点】一次函数的应用;二元一次方程组的应用;一元一次不等式组的应用.
【分析】(1)设甲种材料每千克x元,乙种材料每千克y元,根据题意列出方程,解方程即可;
(2)设生产B产品a件,生产A产品(60﹣a)件.根据题意得出一元一次不等式组,解不等式组即可得出结果;
(3)设生产成本为W元,根据题意得出W是a的一次函数,即可得出结果.
【解答】解:(1)设甲种材料每千克x元,乙种材料每千克y元,
依题意得:
 ,
,
解得:
 ;
;
答:甲种材料每千克25元,乙种材料每千克35元.
(2)设生产B产品a件,生产A产品(60﹣a)件.
依题意得: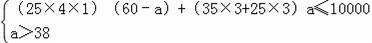
 ,
,
解得:38<a≤
 ;
;
∵a的值为非负整数,
∴a=39、40、41、42;
答:共有如下四种方案:
| A(件) | 21 | 20 | 19 | 18 |
| B(件) | 39 | 40 | 41 | 42 |
(3)生产A产品21件,B产品39件成本最低.理由如下:
设生产成本为W元,则W与a的关系式为:
W=(25×4+35×1+40)(60﹣a)+(35×3+25×3+50)a=55a+10 500,
即W是a的一次函数,
∵k=55>0
∴W随a增大而增大
∴当a=39时,总成本最低;
即生产A产品21件,B产品39件成本最低.
【点评】本题考查了二元一次方程组的应用、一元一次不等式组的应用、一次函数的应用;根据题意中的数量关系列出方程组、不等式组、一次函数关系式是解决问题的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
(1)如图,试用直尺与圆规在平面内确定一点O,使得点O到Rt△ABC的两边AC、BC的距离相等,并且点O到A、B两点的距离也相等.(不写作法,但需保留作图痕迹)
(2)在(1)中,作OM⊥AC于M,ON⊥BC于N,连结AO、BO.求证:△OMA≌△ONB.


查看答案和解析>>
科目:初中数学 来源: 题型:
2011年6月4日,李娜获得法网公开赛的冠军,圆了中国人的网球梦.也在国内掀起一股网球热.某市准备为青少年举行一次网球知识讲座,小明和妹妹都是网球球迷,要求爸爸去买门票,但爸爸只买回一张门票,那么谁去就成了问题,小明想到一个办法:他拿出一个装有质地、大小相同的2x个红球与3x个白球的袋子,让爸爸从中摸出一个球,如果摸出的是红球.妹妹去听讲座,如果摸出的是白球,小明去听讲座.
(1)爸爸说这个办法不公平,请你用概率的知识解释原因.
(2)若爸爸从袋中取出3个白球,再用小明提出的办法来确定谁去听讲座,问摸球的结果是对小明有利还是对妹妹有利.说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com